
Actual Problems in Machine Building. 2015. N 2
Innovative Technologies
in Mechanical Engineering
____________________________________________________________________
60
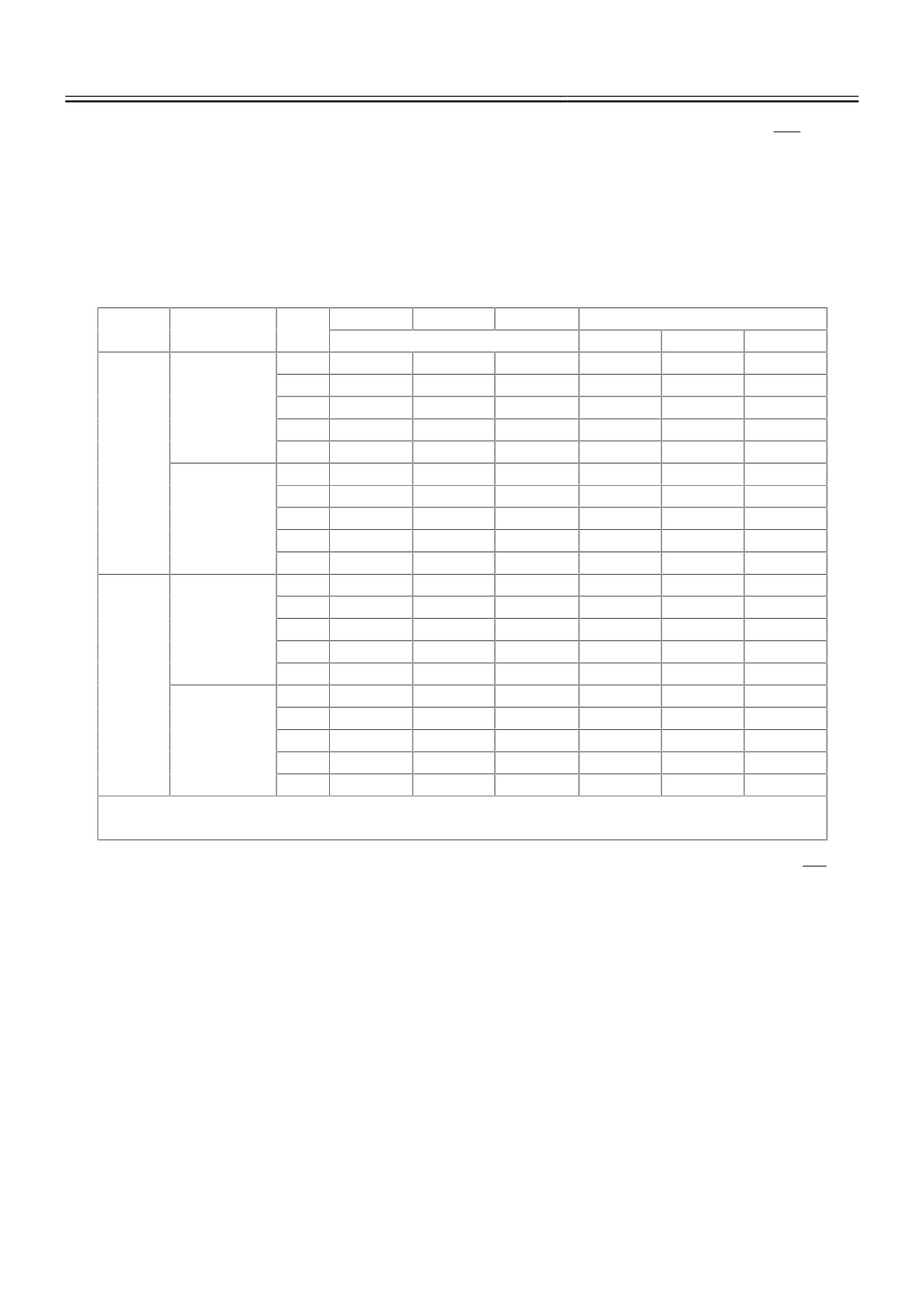
В таблице представлены результаты влияния числа выхаживаний
8;0
j
на
стабильность формирования топографии поверхности в поперечном направлении при
шлифовании кругом 5SG46K12VXP. Анализ полученных данных ведем в условиях
приоритетного отношения к квартильным широтам (КШ) и коэффициентам (3).
Установлено, что выхаживание оказало наибольшее влияние на наибольшие шероховатости.
Оценка влияния числа выхаживания на высотные параметры по мерам рассеяния
Сталь Параметр
j
SD
1j
R
1j
КШ
1j
K
ст
1jp
мкм
p
=1 (1)
p
=2 (2)
p
=3 (3)
Р9М4К8
R
a1
0 0,011 0,04
0,02
1,00
1,00
1,00
2 0,015 0,06
0,02
0,73
0,67
1,00
4 0,017 0,07
0,02
0,65
0,57
1,00
6 0,026 0,11
0,02
0,42
0,36
1,00
8 0,014 0,06
0,01
0,79
0,67
2,00
R
max1
0 0,071 0,25
0,13
1,00
1,00
1,00
2 0,085 0,33
0,10
0,84
0,76
1,30
4 0,133 0,57
0,11
0,53
0,44
1,18
6 0,143 0,60
0,17
0,50
0,42
0,76
8 0,070 0,28
0,06
1,01
0,89
2,17
Р12Ф3К10М3
R
a1
0 0,019 0,08
0,01
1,00
1,00
1,00
2 0,009 0,04
0,02
2,11
2,00
0,50
4 0,010 0,03
0,01
1,90
2,67
1,00
6 0,007 0,03
0,01
2,71
2,67
1,00
8 0,008 0,03
0,01
2,38
2,67
1,00
R
max1
0 0,103 0,43
0,09
1,00
1,00
1,00
2 0,058 0,23
0,05
1,78
1,87
1,80
4 0,054 0,20
0,09
1,91
2,15
1,00
6 0,053 0,23
0,05
1,94
1,87
1,80
8 0,093 0,44
0,07
1,11
0,98
1,29
Примечание: Число выхаживание
j
– 0; 2; 4; 6; 8. Индексы
p
: 1 –
SD
dj
(1), 2 –
R
dj
(2), 3 –
ИКШ
dj
(3)
Так, наименьшая воспроизводимость процесса по всем мерам рассеяния (
3;1
p
)
предсказана при
j
= 6 для БП Р9М4К8. При этом при шлифовании БП Р12Ф3К10М3 по
параметрическим методам предсказаны наибольшие меры рассеяния при
j
= 0:
SD
120
0,019;
R
120
0,08 – для параметра
R
a
1
;
SD
120
0,103;
R
120
0,43 – для параметра
R
max
1
. Оценки стабильности
параметрического метода полностью противоречат результатам по КШ, для которых
оптимальное число выхаживаний для параметра
R
max
1
является:
j
= 8 по для БП Р9М4К8;
j
= 8
для БП Р12Ф3К10М3.
Выводы
1. Проанализированы возможности оценки стабильности процесса шлифования по
квартильным широтам, стандартам отклонений и размахам. Показано, что в условиях
приоритетного использования непараметрического метода статистики наиболее адекватным

















