
Актуальные проблемы в машиностроении. 2015. №2
Инновационные технологии
в машиностроении
____________________________________________________________________
65
ak
R t
4
2
0
,
где
R-
характерный размер источника тепла, м;
k
- коэффициент сосредоточенности
интенсивности источника.
Известно, что для малых промежутков времени, то есть для больших значений
аргумента функции Бесселя, в соотношениях (1) допустима замена
at
rr
at
rr
at
rr I
2
'
2
2
'
exp
2
'
0
.
После преобразований для малых промежутков времени решение, описывающее
тепловой режим в неограниченном теле с отверстием радиуса
r
0
с нормально-тороидальным
источником, при
0 ' ,
'
0
zr r
, получим в виде соотношения
ak
R tа
z r r
ak
R t rr
tzr
4
4
exp
4
8
Q
), ,(
2
2
2
0
2
0
2
.
(3)
Если местное поле учитывает процесс нагрева детали за промежуток времени,
соответствующий одному обороту источника, то общее поле должно учитывать
накапливание теплоты за все время обработки и вызванный этим дополнительный нагрев.
В соответствии с принципом местного влияния допустимо принять, что каждый
отдельно взятый виток источника, предшествующий последнему, определяющему местное
поле,
это мгновенный тепловой импульс, предельно сосредоточенный по направлениям
радиуса и образующей. Основываясь на этом, можно процесс аккумуляции теплоты в теле
представить следующей схемой.
Предположим, что теплоисточник
J
0
(рис.1), определяющий местное поле в области
около диаметрального сечения
z=0
, возникает в момент времени
t=0
. Следовательно,
предыдущий виток источника при угловой скорости
и величиной подачи
S
за один виток
источника (на схеме – мгновенный кольцевой источник
J
1
) завершился раньше в момент
времени
/2
1
t
на расстоянии
S z
1
от источника
J
0
.
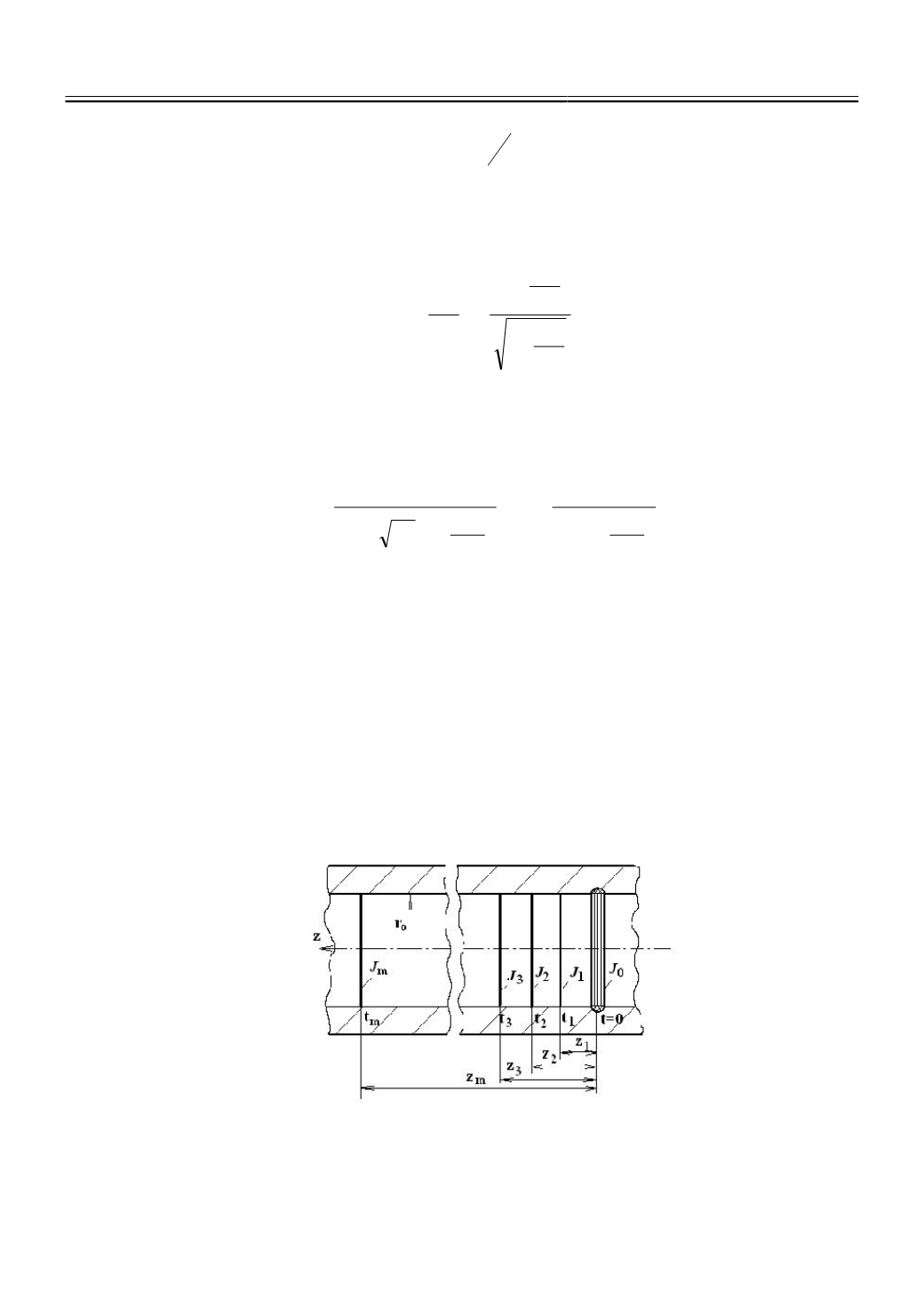
Рис.1.
Схема к расчету аккумуляции теплоты в теле с отверстием.
Еще раньше в момент времени
1
2
2
t
t
и на расстоянии
1
2
2
z
z
действовал
кольцевой источник
J
2
,
и так далее вплоть до первого мгновенного кольцевого импульса
J
m
,

















