
Actual Problems in Machine Building. 2015. N 2
Innovative Technologies
in Mechanical Engineering
____________________________________________________________________
154
совместно для всех компонентов сборки вокруг мест разъемных соединений корпусов –
замков. Таким образом, величина припуска на механическую обработку корпуса в сборе
должна быть достаточной для устранения всех погрешностей возникших на
предшествующих этапах изготовления и на этапе установки заготовки. Согласно
общепринятому подходу определение величины припуска ведется на основе значения
минимального припуска [4, 6, 8], который в случае поверхности вращения может быть
найден из выражения:
2
2
min
, ì ì ;
z
z
R h
(1)
где
R
z
– шероховатость обрабатываемой поверхности, мм;
h
– глубина дефектного слоя
обрабатываемой поверхности, мм;
δ
– суммарные отклонения формы и расположения
обрабатываемой поверхности, мм;
ε
– погрешность установки заготовки, мм.
Величины
R
z
и
h
формируются на этапе термической резки и полностью
определяются её технологией. Величина
ε
определяется способом установки заготовки и
использующимися при этом средствами технологического оснащения.
Наиболее сложной и, как будет показано ниже, наиболее значимой составляющей
является
δ
. Это связано с тем, что отклонения обрабатываемой поверхности формируются на
всех предшествующих этапах изготовления корпуса. Величина
δ
в первую очередь
определяется допусками на изготовление компонентов сборки и допусками на размеры и
расстояния в процессе сборки-сварки корпуса. В целом формирование погрешностей сходно
с механизмом, рассмотренным в работе [9]. Представим схематично формирование
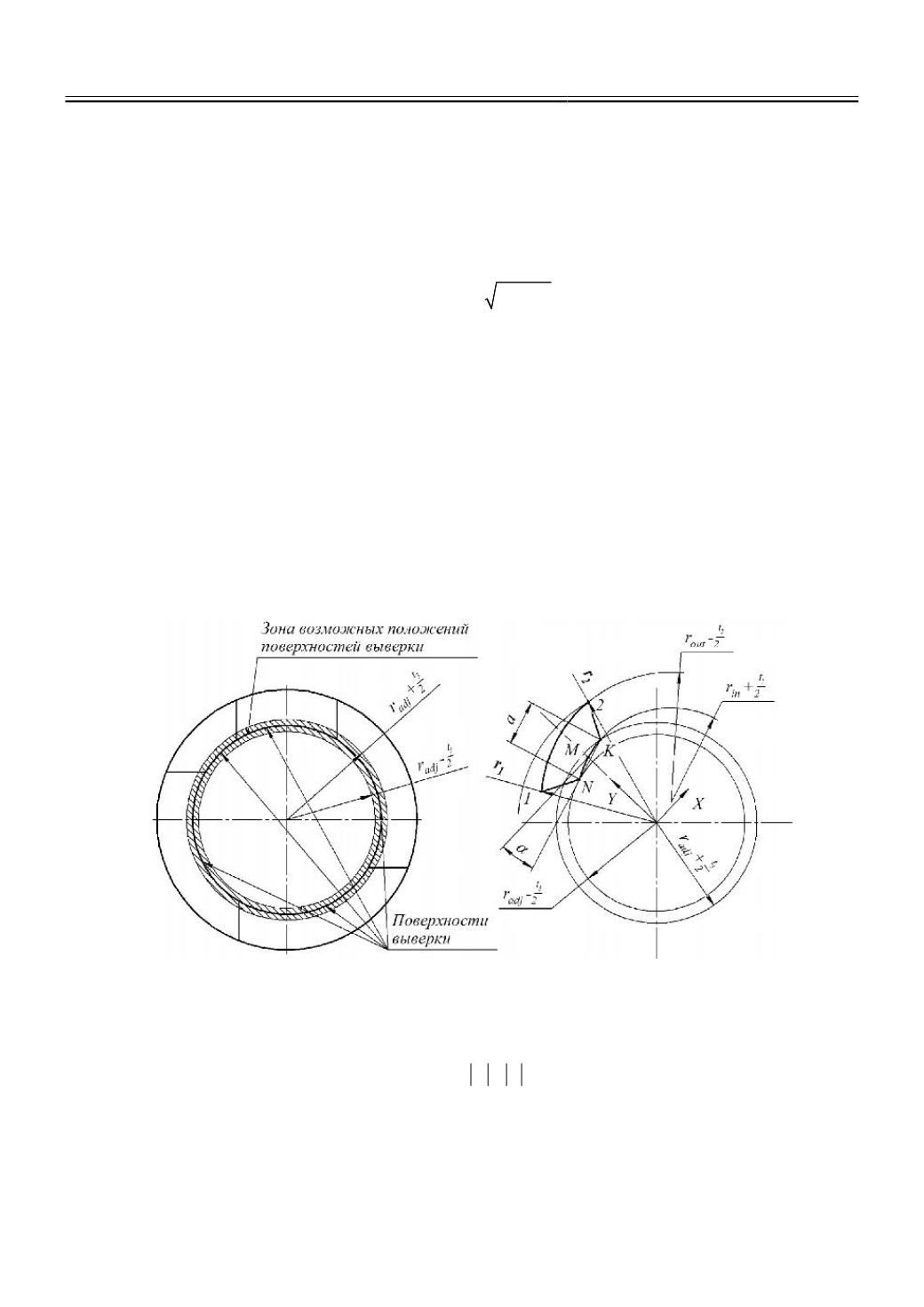
отклонений обрабатываемой поверхности (рис. 3).
Величина отклонения в наиболее неблагоприятном случае может быть найдена как
разность модулей радиус-векторов точек 1 и 2:
2
1
.
r r
(2)
Для определения радиус-векторов совместим начало системы координат с центром
окружности выверки и составим матрицу поворота относительно центра M в однородных
координатах. В таком случае координаты радиус векторов могут быть найдены из
выражения:
Рис. 3.
Расчетная схема к определению отклонений

















