
Актуальные проблемы в машиностроении. 2015. №2
Инновационные технологии
в машиностроении
____________________________________________________________________
105
В полученном уравнении коэффициенты
A
и
B
определяются:
2
2
4
1
2
2
4
1
22
21
12
11
2
22
21
2
12
11
22
21
12
11
22
21
12
11
2
22
21
2
12
11
22
21
12
11
cos
k k k k
k k
k k
k k
k k
B
cos
k k k k
k k
k k
k k
k k
A
,
(3)
где
11
11
1
R k
,
12
12
1
R k
,
21
21
1
R k
,
22
22
1
R k
− кривизна поверхности
первого и второго тела в главных нормальных сечениях;
– угол между главными
плоскостями, в которых определяем кривизну
k
11
и
k
21
.
Принятое между точками
A
1
и
A
2
расстояние до деформации
z
1
+
z
2
, а величину его
изменение после деформации (
w
1
(0)−
w
1
)+ (
w
2
(0)−
w
2
), то при сжатии тел силами,
действующими вдоль общей оси
z
, в соприкосновение придут точки тел, которым
соответствует равенство:
z
1
+
z
2
= (
w
1
(0)−
w
1
)+ (
w
2
(0)−
w
2
) = (
w
1
(0)+
w
2
(0)) − (
w
1
+
w
2
),
(4)
где
w
1
(0)+
w
2
(0)=
− сближение точек.
Тогда
z
1
+
z
2
=
− (
w
1
+
w
2
).
Полученная зависимость является уравнением перемещений контактной задачи.
Среди всех точек, приходящих в соприкосновение при деформации тел, величина
z
1
+
z
2
будет
наибольшей у контурных точек площади контакта.
Учитывая, что размеры площадки контакта малы по сравнению с общими размерами
соприкасающихся тел, была применена зависимость для определения упругих перемещений
каждого из контактирующих тел:
F
dF
r
p
w
1 1
;
F
dF
r
p
w
2 2
,
(5)
где
F
– площадь контакта, ограниченная эллипсом;
r
− расстояние от точки, в которой
определяют перемещение
w
, до точки приложения элементарной силы
;
1
2
1
1
1
E
и
2
2
2
2
1
E
− коэффициенты упругих свойств материала первого
и второго тела;
1
,
2
− коэффициенты Пуассона первого и второго тела;
Е
1
,
Е
2
− модули
упругости первого и второго тела.
p
0
A
0
O
x
a
b
p(x,y)
y
dr
r
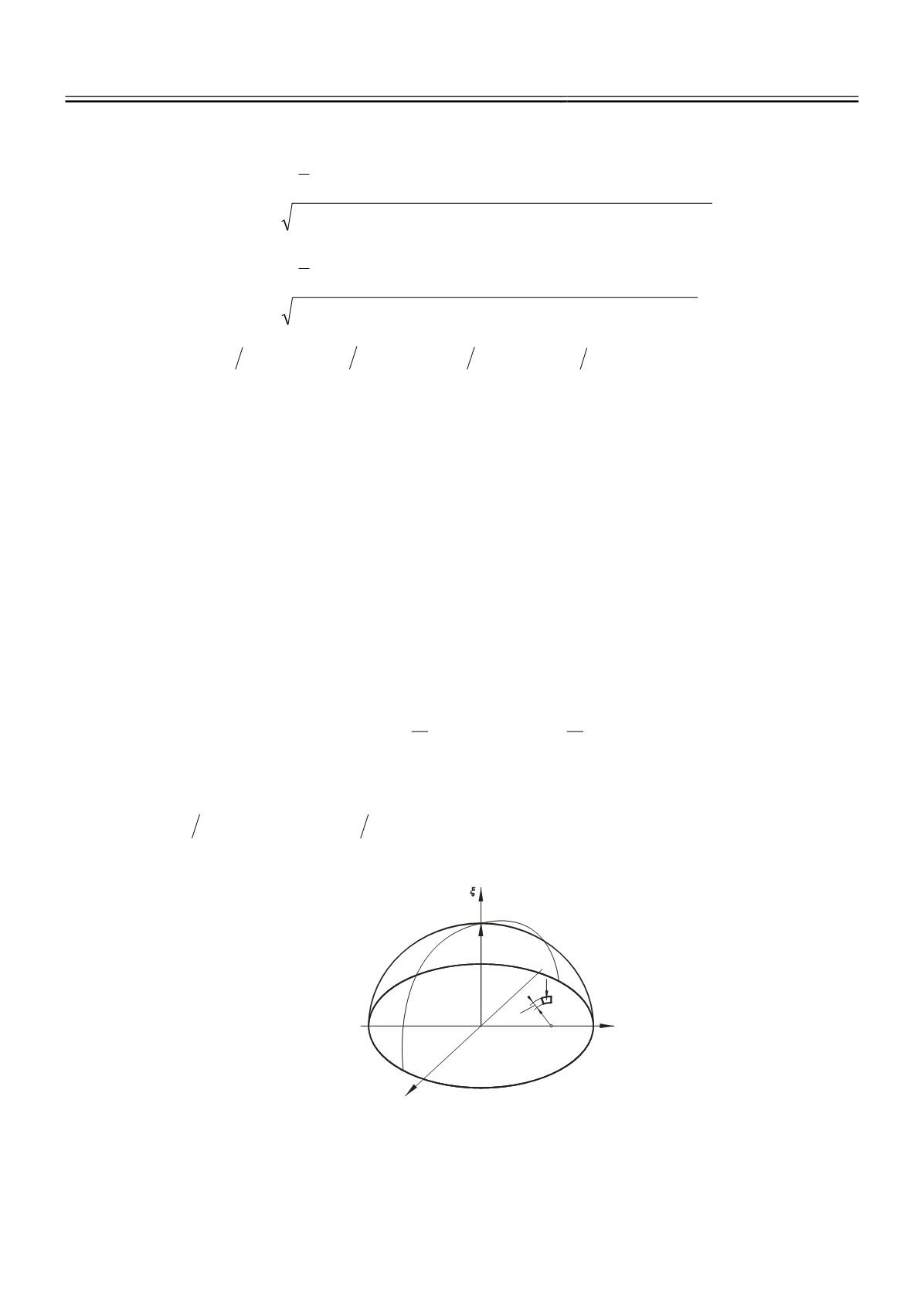
Рис. 3.
Эпюра распределения контактных давлений
под воздействием сжимающей силы
P
Используя зависимости упругих перемещений для каждого из тел, уравнение
перемещений можно представить

















