
Механики XXI веку. №15 2016 г.
126
)
(
))
( 90 cos(
)
)
cos(
)
sin(
cos(
)
)
cos(
)
sin(
cos(
oz tgb
arctg
Ф
oz tgb
dr oor
dr
arctg
oor
dr oor
dr
arctg
dr X
(3)
)
(
))
(
90 sin(
)
)
cos(
)
sin(
cos(
)
)
cos(
)
sin(
cos(
0
oz tgb
arctg
Ф
oz tgb
dr oor
dr
arctg
oor
dr oor
dr
arctg
dr Y
b Z
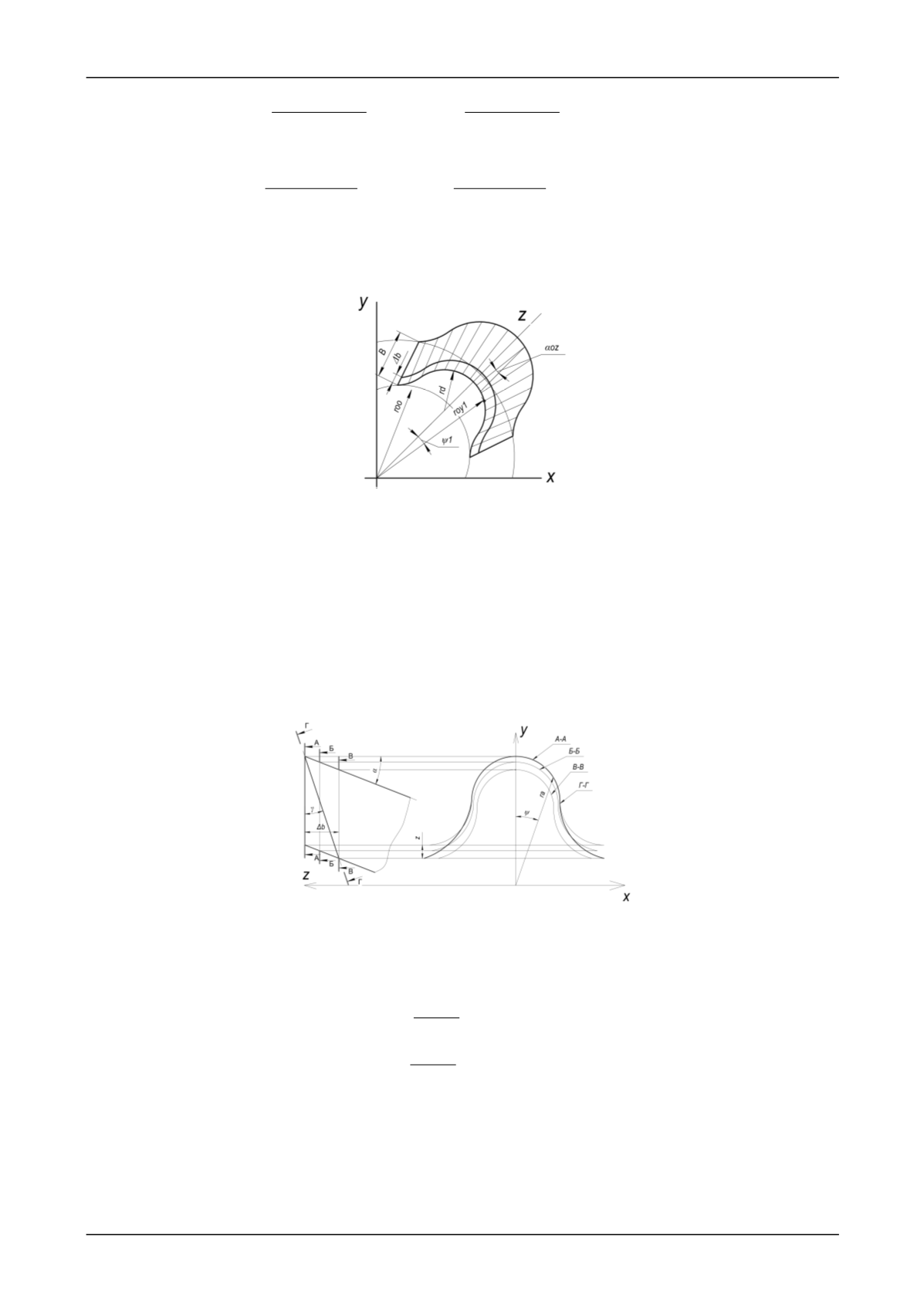
На рисунке 2 изображена задняя поверхность долбяка циклоидального профиля
Рис.2. Задняя поверхность долбяка циклоидального профиля
Благодаря математическим выражениям (3) мы можем рассчитать координаты точек профиля
любого торцевого сечения долбяка отличающегося от исходного на величину
b
[2].
Винтовая задняя поверхность долбяка дает математически верный профиль только в сечени-
ях, перпендикулярных оси долбяка. Так как передняя поверхность долбяка является конической по-
верхностью, то она пересекает боковые поверхности зуба долбяка под углом 90
о
-
В
к его оси.
Вследствие этого боковая режущая кромка долбяка, образующаяся как след пересечения конической
передней и боковой винтовой поверхности, отклоняется на некоторую величину. Угловое коррегиро-
вание, применяемое для долбяков эвольвентного профиля, принципиально не применимо для цик-
лоидального ввиду геометрических особенностей.
Рис.3. Определение отклонений профиля взависимости от переднего угла
Поэтому для определения отклонений представим режущее лезвие долбяка как результат пе-
ресечения задней винтовой поверхности с конической передней (см. рис.3). Математически передняя
поверхность представлена выражением (4):
b z
tg
b ra Y
tg
b ra X
sin
cos
(4)
где
ra
– радиус – вектор в точке профиля;
– боковой задний угол;
b
– изменение координат по
оси
z
;
– передний угол.
Решая уравнения передней и задней поверхности, мы можем найти координаты всех точек
профиля долбяка и по этим точкам определить отклонение
z
(рис.3) при любом переднем угле и
скорректировать профиль с учетом этих отклонений.














