
Современные технологии и автоматизация в машиностроении
125
В работе [3] подробно представлена методика профилирования долбяков циклоидального
профиля. Данная методика основана на трехмерном математическом отображении схемы резания.
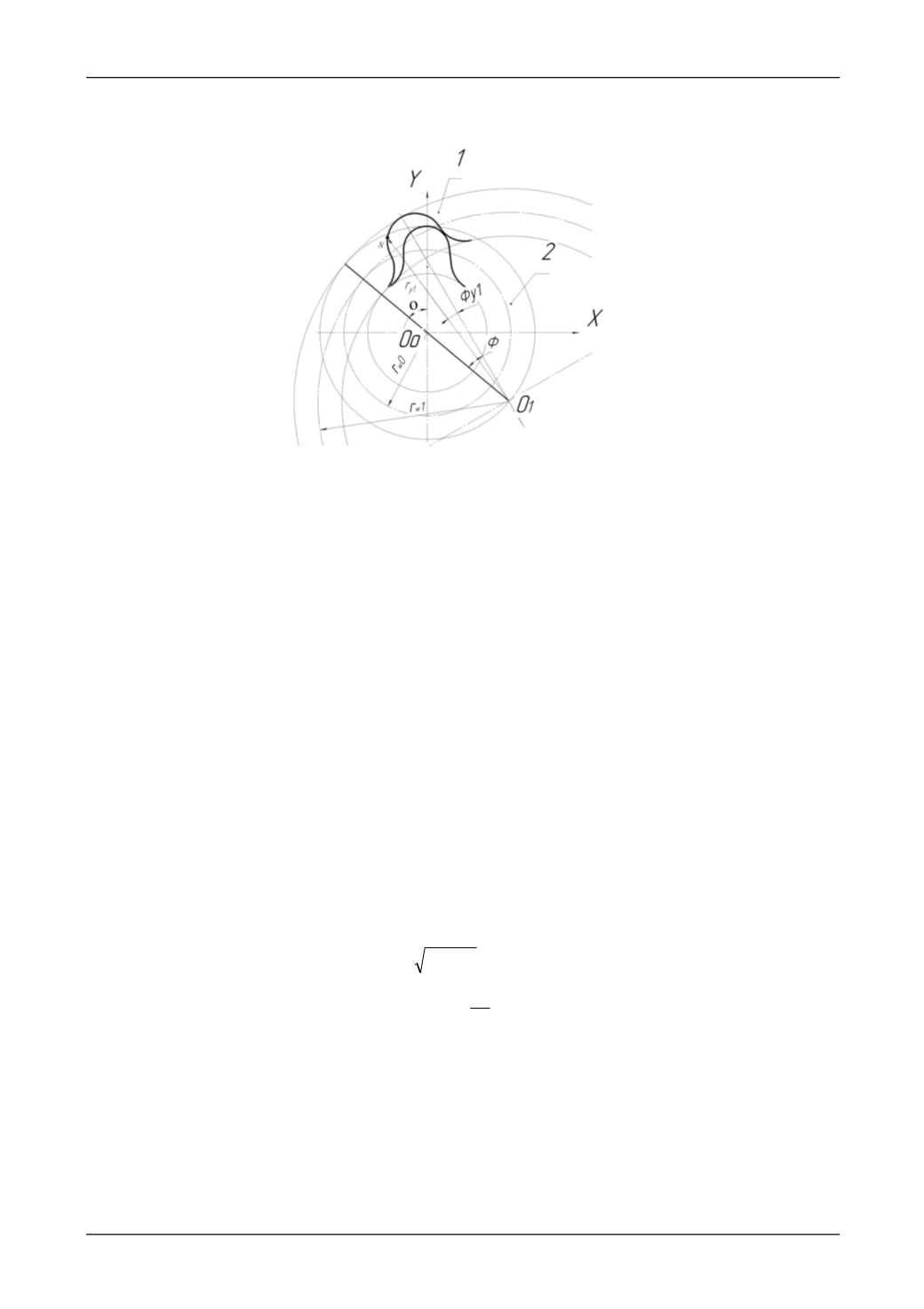
Рис. 1. Определение положения впадины колеса
с внутренними зубьями 1 относительно зуба долбяка 2
Процесс формообразования или обработка зубчатой поверхностью 1 профиля долбяка 2 (рис.
1), представлен выражением, описывающим положение каждой точки профиля впадины колеса в лю-
бой момент обработки.
Исходными данными при профилировании долбяка являются профиль впадины, количество
зубьев
1
z
, радиус основной окружности
1
rb
, радиус окружности выступов
1
ra
и радиус окружности
впадин
1
rf
зубчатого колеса с внутренними зубьями, количество зубьев долбяка
0
z
.
Уравнение траектории перемещения любой точки впадины зубчатого колеса с внутренними
зубьями относительно долбяка получим, проектируя отрезки
1
OoO
и
OoN
на координатные оси (рис.
1):
,
)
()1 ( cos
)
(
cos
)
()1 ( sin
)
(
sin
1
1
1
1
1
1
1
1
l Z
ФФ U r ФФU a Y
ФФ U r ФФU a X
y
y
w
y
y
w
(1)
где
w
a
- межосевое расстояние долбяка и зубчатого колеса с внутренними зубьями,
1
U
- отношение
числа зубьев колеса к числу зубьев долбяка,
Ф
– угол определяющий положение впадины колеса от-
носительно межосевого расстояния,
Ф
- элементарный угол поворота за время двойного хода дол-
бяка,
0
r
- радиус делительной окружности долбяка,
1
y
r
- радиус – вектор точки на впадине зубчатого
колеса с внутренними зубьями;
1
y
- угол между радиус – вектором точки впадины зубчатого колеса
с внутренними зубьями и осевой линией.
Параметры
1
y
r
и
1
y
определяются из выражений:
1
1
2
2
1
arcsin
y
i
y
i
i
y
r
x
y x
r
(2)
где
i
x
и
i
y
координаты точки профиля впадины зубчатого колеса с внутренними зубьями.
Профиль впадины зубчатого колеса с внутренними зубьями задается в торцевом сечении[3].
Решая задачу профилирования, перед нами встает не менее актуальная задача выявления за-
кономерностей изменения профиля взависимости от значений передних и задних углов. Для решения
данной задачи представим математически заднюю винтовую и переднюю коническую поверхности.
В общем виде уравнение задней поверхности циклоидального долбяка представлено следую-
щим математическим выражением [2]:














