
Actual Problems in Machine Building. 2015. N 2
Materials Science
in Machine Building
____________________________________________________________________
422
решению задач прочностного анализа или теплообмена в структурно-неоднородной среде,
какую представляют собой конструкции из композиционных материалов. Подобная
модификация алгоритма может быть полезна для исследовательских целей.
Теория
Метод конечных элементов основан на идее замены непрерывной функции
(температуры, механического напряжения и др.) дискретной моделью, которая строится на
множестве кусочно-непрерывных функций. При этом геометрическое представление
исследуемой конструкции осуществляется с помощью набора областей с канонической
геометрией (отрезки, многоугольники, многогранники) – так называемых, конечных
элементов.
Очевидно, что построение конечно-элементной модели некоторой области
физического пространства в общем случае не зависит от значения неизвестной функции.
Дизъюнктивность конечных элементов, являющаяся их фундаментальным свойством [5],
открывает дополнительные широкие возможности программирования решения. В частности,
для исследования поведения любой области материала можно выделить типичный конечный
элемент, аппроксимировать на нем поле температур (или напряжений) и полностью описать
поведение элемента с помощью этой аппроксимации независимо от его положения в модели,
характера связей с примыкающими к нему элементами и поведения других элементов
модели.
Неизвестная функция аппроксимируется на каждом из конечных элементов так
называемой, пробной функцией (как правило, полиномом). Причем эти пробные функции
удовлетворяют граничным условиям непрерывности, совпадающим с граничными
условиями, налагаемыми решаемой краевой задачей. Выбор для каждого элемента
аппроксимирующей функции определяет соответствующий тип элемента. В задачах
механики и теплотехники, как правило, достаточно обеспечить лишь непрерывность
функции, поэтому наиболее часто применяются элементы лагранжевого типа.
Рассмотрим особенности построения матричного алгоритма решения задачи
теплопроводности в много компонентной среде, с использованием двумерных симплекс-
элементов, представляющих особый интерес для разработчиков собственных программ
автоматизированного проектирования.
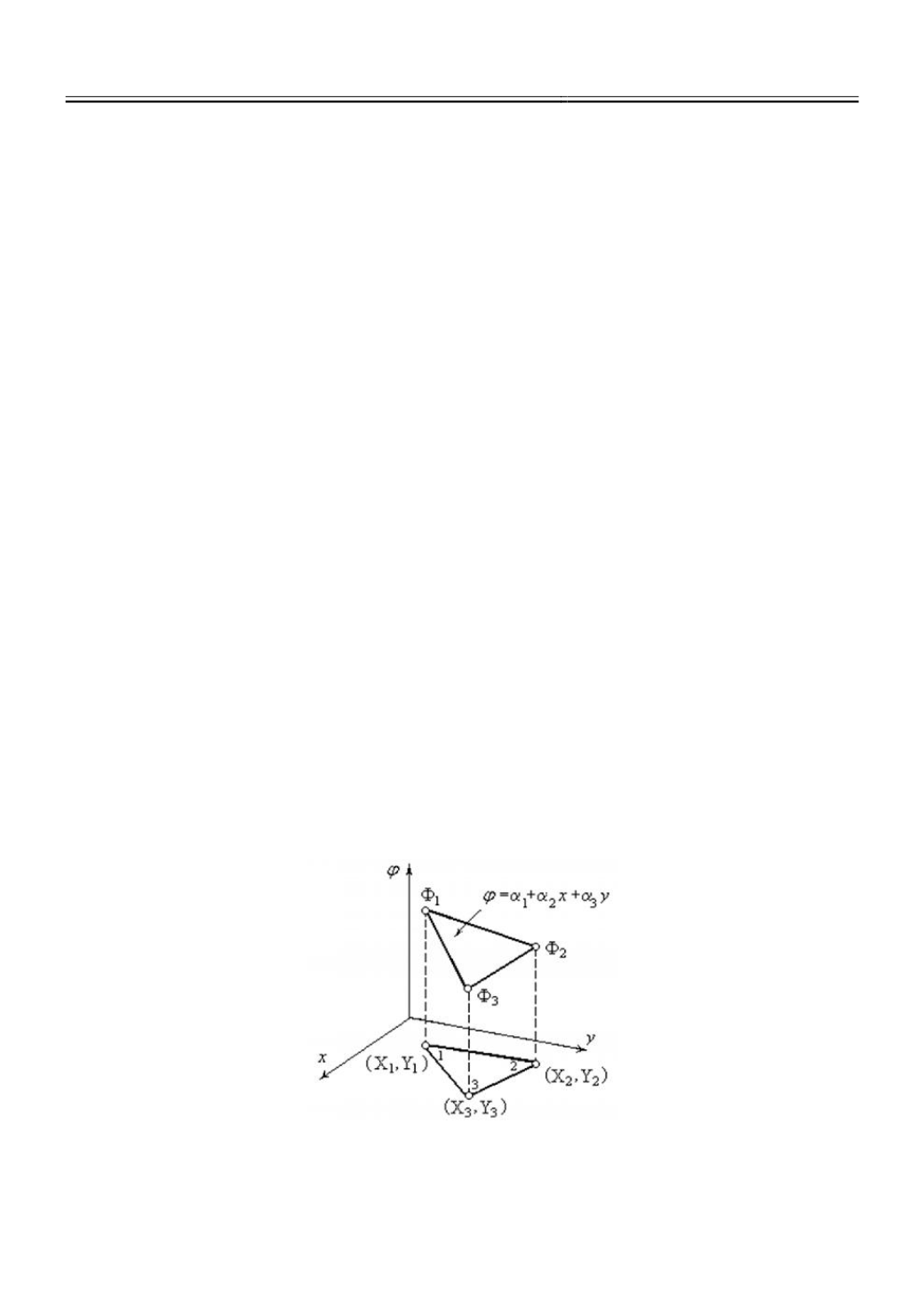
Двумерный симплекс-элемент представляет собой треугольник с прямолинейными
сторонами и тремя степенями свободы, по одной в каждой вершине (рис. 1).
Рис.1
. Симплекс-элемент
Интерполяционный полином в этом случае имеет вид

















