
Материаловедение, динамика и прочность машин и механизмов
297
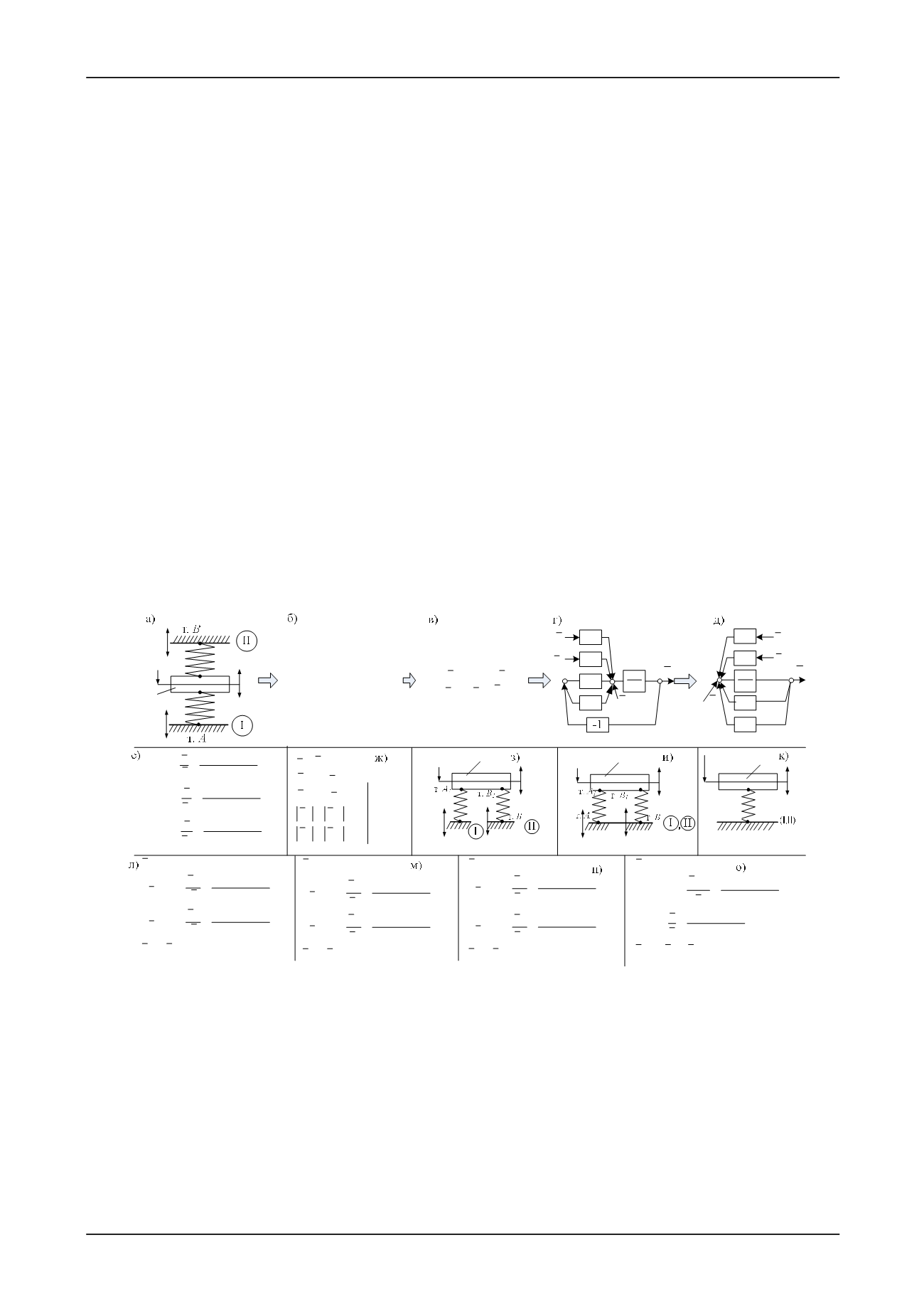
Структурное математическое моделирование.
На рис. 3 представлена методика определе-
ния динамических реакций связей в механических колебателныч системах с одной степенью свобо-
ды.
Последовательный переход от позиции а до позиции о рис. 3. Стадии преобразований исход-
ных математических моделей приведены также на позициях (3)–(25). Для реализации методики опре-
деления реакций в выбранных точках на основе расчетной схемы (рис. 3а) составляется дифференци-
альное уравнение (3), которое трансформируется после преобразований Лапласа в уравнение (4), а
затем – в структурные схемы на рис. 3 г,д. При этом
p = jω
– комплексная переменная, а значок (–)
над переменными означает изображение по Лапласу. Физическая сущность метода заключается в
том, что объект защиты при действии различных возмущений выделяется на структурной схеме как
звено с передаточной функцией типового интегрирующего звена второго порядка. В свою очередь
типовые элементы виброзащитной системы представляют собой элементы структурной теории в сле-
дующих связях: пружина – звено с передаточной функцией усилительного звена; демпфер – звено с
передаточной функцией дифференцирующего звена; промежуточный массоинерционный элемент –
звено с передаточной функцией дифференцирующего звена второго порядка. Динамическая реакция
представляет собой произведение приведенной динамической жесткости в заданной точке на ее ко-
ординату смещения. Приведенная динамическая жесткость фомируется цепью отрицательной обрат-
ной связи относительно объекта защиты, что достигается преобразованиями, правила которых харак-
терны для аппарата теории автоматического управления. Для удобства пользования рис. 3 приведен
на отдельном листе. Более подробное изложение методики определения динамических реакций при-
водится в статьях [6,7].
Математическое моделирование и определение динамических реакций в механических
колебательных системах с двумя степенями свободы
. В данном докладе излагаются основные по-
ложения методики определения именно динамических реакций. В практических задачах вибрацион-
ной защиты движения объекта рассматриваются как малые колебания относительно положения ста-
тического равновесия.
tQ
tz
2
m
y
2
k
1
k
tz
1
1 2
1 1 2 2
(
)
( );(3)
my k k y
k z k z Q t
2
1 2
1 1 2 2
(
)
;(4)
mp y k k y
k z k z Q
1
k
2
k
1
k
2
k
2
1
mp
y
2
z
1
z
Q
1
k
2
k
1
k
2
k
2
1
mp
y
2
z
1
z
Q
1
2
1 2
1
2
2
1
1 2
2
3
2
2
1 2
1
( )
,(5)
( )
,(6)
( )
,(7)
y
W p
Q mp k k
k
y
W p
z mp k k
k
y
W p
z mp k k
1
1
2
1
1
( ),(8)
,(9)
,(10)
,(11)
,(12)
A
B
A A
B B
y Q W p
R k y
R k y
R R
R R
1
2
0
0
0
Q
z
z
Q
m
y
2
k
1
k
1
z
2
z
Q
m
y
2
k
1
k
2
1
z z z
z k k
)
(
2
1
m
y
2
1
k k
0
Q
1
2
1
2
1 2
2
2
1 2
0.
0.
0,(13)
( )
,(14)
( )
,(15)
,(16)
A
B
A
R
B
R
A B
Q z
z
R
k
W p
Q mp k k
R
k
W p
Q mp k k
R R
1 2
2
1
2
1
1 2
1 2
2
1
1 2
0.
0.
0,(17)
( )
,(18)
( )
,(19)
,(20)
A
B
A
R
B
R
A B
Q z
z
k
R
W p
z mp k k
R
k k
W p
z mp k k
R R
1 2
1 2
2
2
1 2
2
2
2
2
1 2
0.
0.
0,(21)
( )
,(22)
( )
,(23)
,(24)
A
B
A
R
B
R
A B
Q z
z
R
k k
W p
z mp k k
k
R
W p
z mp k k
R R
,
1 2
,
1 2
2
1 2
1 2
2
1 2
,
0.
,(25)
( )
,(26)
( )
,(27)
,(28)
I II
I II
R
I I
A B
Q z z z
R
k k
W p
z
mp k k
k k
y
W p
z mp k k
R R R
1
т.
B
1
т.
A
Рис. 3. Принципиальные позиции метода определения динамическиз реакций
Вместе с тем, статическая нагрузка в ВЗС формирует соответствующие статические реакции.
Полная реакция в характерных или выбираемых точках определяется суммой двух компонент. При
равенстве нулю полной реакции в точках возможно возникновение зазоров при неудерживающих
связях, что требует в случае необходимости соответствующего контроля за величинами реакции.
Особенности определения статических реакций рассмотрены в работе [8].
В системах с двумя степенями свободы методика определения динамических реакций остает-
ся прежней, то есть выделяется объект защиты, внешние силы приводятся к объекту, производятся
структурные преобразования, в рамках которых формируется цепь обратной отрицательной связи
относительно объекта защиты, представленного интегрирующим звеном второго порядка. Коэффи-














