
Механики XXI веку. №15 2016 г.
286
В предлагаемой статье рассматривается возможность разработки обобщенных подхо-
дов в решении задач динамических взаимодействий элементов технологических систем с не-
удерживающими связями.
Общие положения. Постановка задачи. Математическое моделирование.
Развивается
обобщенный подход к оценке характеристик траекторий движения частиц с формированием фазы
свободного подлета с последующим взаимодействием с вибрирующей поверхностью. В качестве ис-
ходной используется математическая модель взаимодействия материальной частицы с горизонталь-
ной поверхностью рабочего органа, колеблющейся по гармоническому закону
)
sin(
)(
t
A tH
(рис.1).
Рис. 1. Принципиальная схема взаимодействия материальной частицы с вибрирующей поверхностью
Основные элементы разработанной математической модели представлены в таблице: система
дифференциальных уравнений для семейства возможных траекторий в фазе полета в зависимости от
параметра (I, таб.), функция зазора (рис.2) между формой движения единичной частицы и формой
поверхности колебания (II, таб.), условия отрыва частицы от вибрирующей поверхности (III, таб.).
Таблица.
Элементы математической модели
I. Система диф. ур.
II. Функция зазора
III.Условия отрыва
)
sin(
) ,(
)
cos(
) ,(
,
) ,(
0
0
0
0
0
2
0
2
0
0
t
A
tt X
t
A
t
tt X
t tg
t
tt X
t t
H
t t
H
H
.
,)
(
2
1
)
cos( )
(
)
sin(
)
sin(
) ,(
0
2
0
0
0
0
0
t t
t tg
t
t t A
t
A
t
A tt R
H
0 ) ,(
,0 ) ,(
0
0
0
0
t t
k
H
k
t t
i
H
i
t
tt R
k i
t
tt R
Развития подхода реализуется введением понятие обобщенной функции зазора, позволяющей
вести детализированное исследование наиболее значимых свойств вибрационных взаимодействий
элементов с учетом неудерживающих связей без конкретизации формы колебания опорной поверх-
ности.
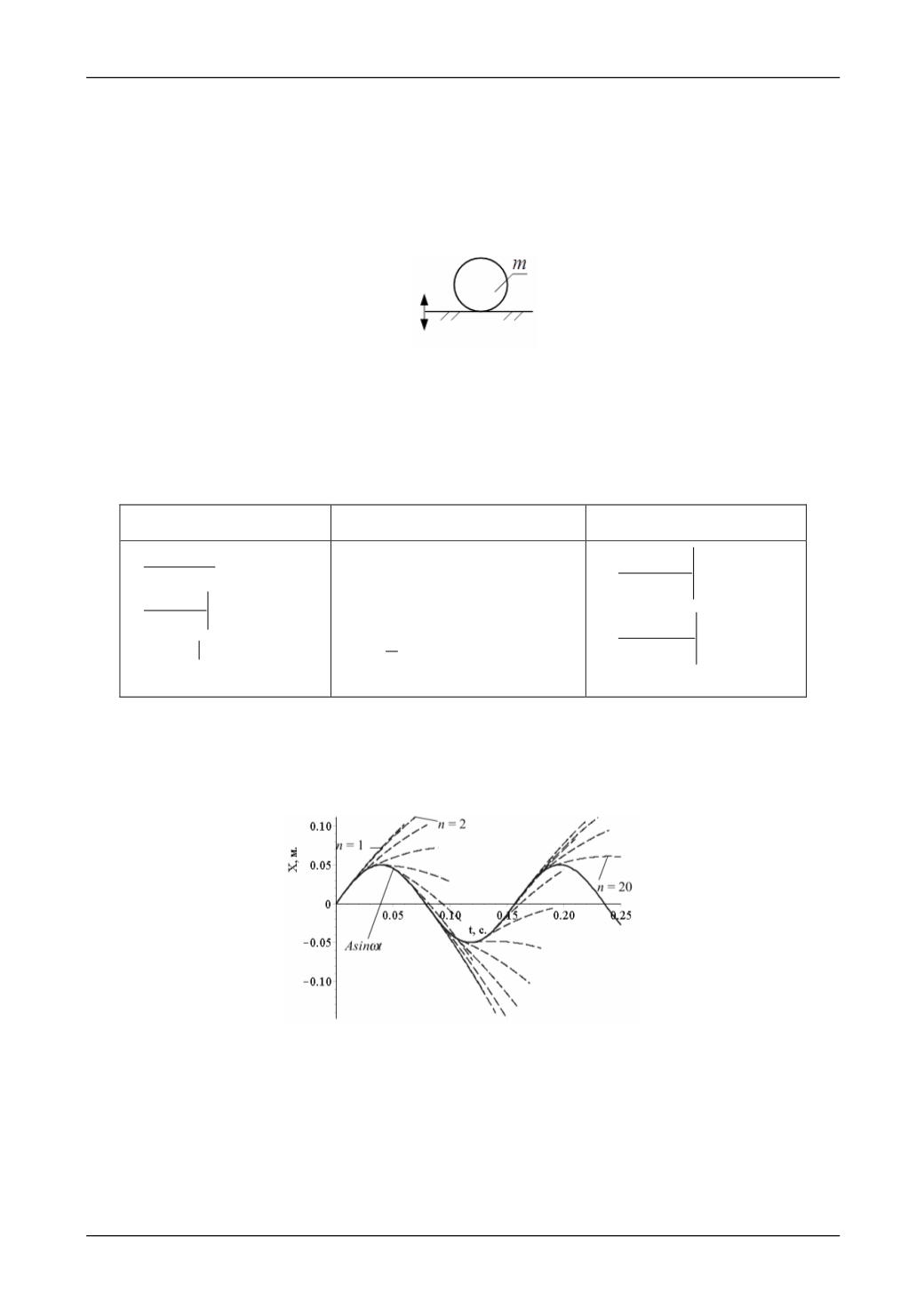
Рис. 2. Семейство возможных траекторий:
)1 (01,0
0
n
t
с, где
n
= 1..20,
A
= 0,05 м,
40
рад/c
В рамках представлений о функции зазора условия отрыва материальной частицы с учетом
неудерживающих связей определяются не только положением частицы или фазовыми параметрами
гармонического процесса, но и соотношениями между смещением, скоростью, ускорением и резко-
стью (III, таб.). Разработанный аппарат функции зазора позволяет определять условия формирования
рациональных режимов с заданной структурой вибрационного поля, выступающего ключевой харак-
теристикой динамического качества работы вибрационной технологической машины с учетом требо-
ваний однородности и одномерности [9].














