
Механики XXI веку. №15 2016 г.
134
Калибровка камеры – это задача получения внутренних и внешних параметров камеры по
имеющимся фотографиям или видео, отснятыми ею. Калибровка камеры часто используется на на-
чальном этапе решения многих задач компьютерного зрения и в особенности дополненной реально-
сти [1, 2]. При решении данной задачи необходимо определить внутренние параметры системы – ко-
ординаты точки пересечения оптической оси объектива с предметной плоскостью, а также расстоя-
ние от картинной плоскости до оптического центра и коэффициент преобразования между единицами
измерения в картинной и предметной плоскости.
К настоящему моменту разработано достаточно большое число методов калибровки камеры.
В работах [3, 4] в качестве объекта калибровки используется круг, расположенный в плоскости, кото-
рая параллельна плоскости изображения камеры. Указанный метод не предполагает прямой связи
между снимаемым изображением и параметрами калибровки камеры. В [5] калибровка камеры про-
изводится с использованием плоского шестиугольника, границами которого являются три пары па-
раллельных прямых. Анализ описанной методики установил, что она работает невполне надежно, так
как точность определения параметров калибровки в зависимости от положения шестиугольника и
камеры имеет относительно большую погрешность. Таким образом, целью исследования является
разработка усовершенствованной методики калибровки камеры, отличающейся более высокой на-
дежностью. В указанной методике в качестве калибровочного тела используется квадрат, распола-
гающийся в предметной плоскости. Преимущество данной методики заключается в том, что она це-
ликом основана на математическом аппарате проекционной геометрии, что позволило увеличить на-
дежность. Увеличение надежности связано с тем, что в расчетах отпала необходимость использова-
ния сложных комбинаций тригонометрических функций.
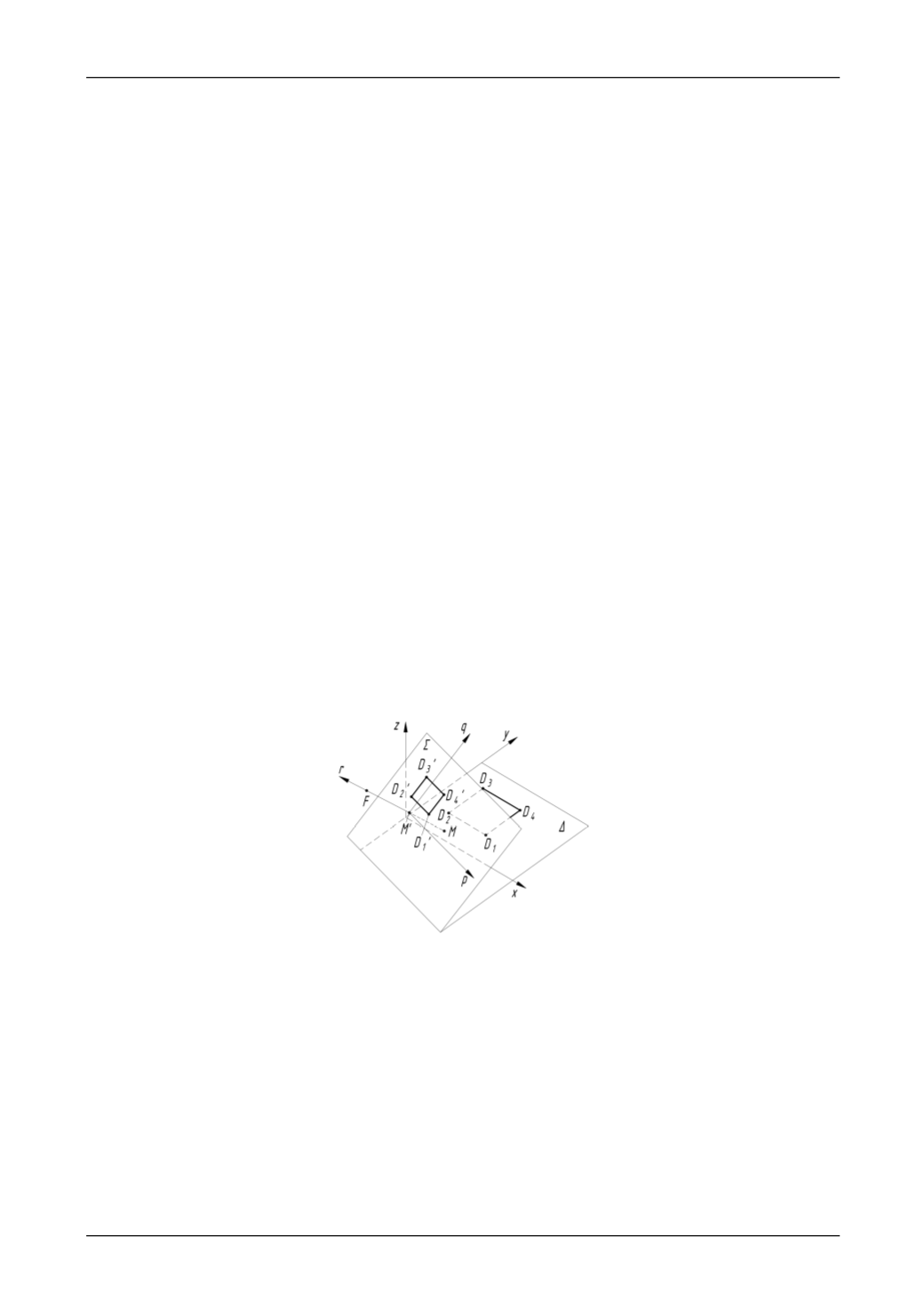
Пусть предметная система координат и система координат изображения ортогональны и за-
даются соответственно осями
zyx
, ,
и
rqp
, ,
(в соответствии с рисунком 1). Имеется некоторый
квадрат
4 3 2 1
DDDD
, располагающийся в координатной плоскости
, инцидентной осям
x
и
y
.
Данную плоскость будем называть предметной плоскостью [6]. Стороны этого квадрата параллельны
координатным осям x и y. Изображение квадрата
4 3 2 1
DDDD
находится в картинной плоскости
.
Центр проецирования, совпадающий с оптическим центром, пусть размещается в точке
F
, а ось объ-
ектива совпадает с осью
r
системы координат изображения. Остальные оси системы координат изо-
бражения (
p
и
q
) располагаются в картинной плоскости
и направлены параллельно границам
кадра.
Рис. 1. Предметная система координат
zyx
и система координат изображения
rqp
Пусть
M
– основание перпендикуляра, опущенного из
F
на картинную плоскость
, и од-
новременно – начало системы координат изображения. Данная точка является точкой пересечения
оптической оси объектива с картинной плоскостью. Расстояние от
F
до
M
есть расстояние от цен-
тра проецирования
F
до картинной плоскости. Обозначим его длину буквой
t
. Пусть
n
– коэффи-
циент преобразования между единицами измерения изображения (картинной плоскости) и предмет-
ной плоскости. Через
M
обозначим точку пересечения оси
r
с предметной плоскостью, а расстоя-
ние между
M
и
M
обозначим через
d
. Буквой κ обозначим угол между оптической осью камеры и
предметной плоскостью (далее – угол тангажа) [7].
Поставим задачу определить внутренние параметры камеры: расстояние t от оптического цен-
тра камеры до картинной плоскости [8]; коэффициент n преобразования между единицами измерения
картинной плоскости и предметной плоскости [9, 10].














