Актуальные проблемы в машиностроении. 2016. №3

482 / 530

Actual Problems in Machine Building. 2016. N 3 Materials Science
in Machine Building
____________________________________________________________________
482
Из выражения (17)
 
 
1 2
1 2
lg
lg
dd
PP m
 (18)
Следует отметить, что    
1 2 1 2lg lg PP PP  , а    
1 2 1 2lg lg aa dd , где
  ; 2 2 2
2
i i i hc hRc a  
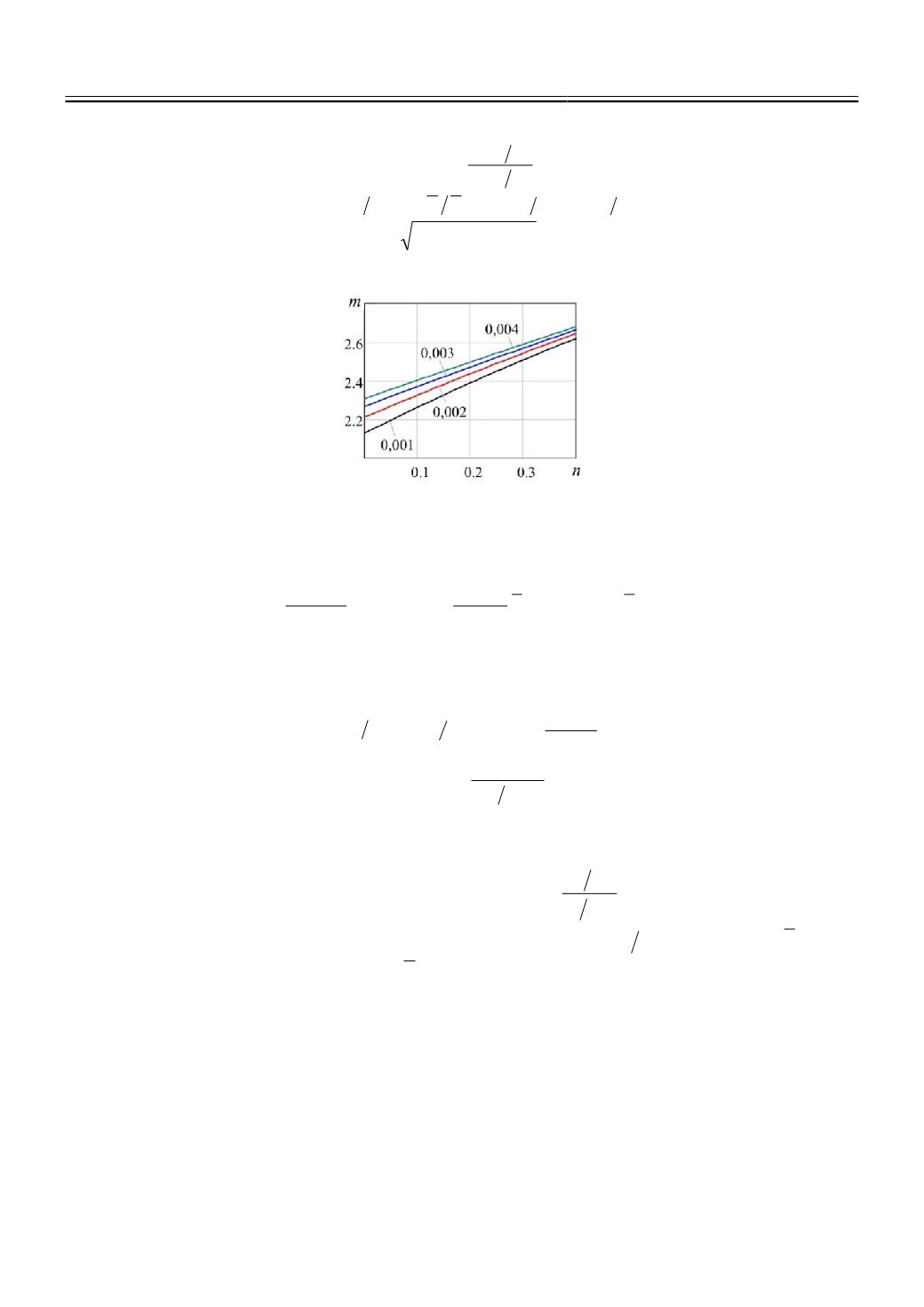
Зависимости индекса Майера от экспоненты упрочнения представлены на рис. 1.
Рис. 1. Зависимость индекса Майера m от экспоненты упрочнения для разных значений εy.
Если закон Майера представить в виде (12), то константа  
n BB
y ,   определяется
выражением      
     
nym
z y r
nyA
nyB
y E
y hn a h e n B
E
n B , ,
2
,
* , , ,
,   
 


  
 (19)
С помощью константы  
n B
y ,  осуществляется переход от диаграмм твердости к
диаграммам растяжения и наоборот.
Если деформация описывается зависимостью (9), то
  ; 2 n m     n
u
n
y u
u
u в E
Dd  

    1
*
) ( (20)
  ;
1

 

в
n n
y
Dd
n n (21)
так как согласно данным [12] . n
u 
Подставляя выражение (21) в (9), получим
   
  . 1 1

 






 
в
n n
u p
n n
u Ra
Ra n n (22)
На рис. 2 представлены зависимости деформации от Ra a
r  (рис. 2а) и от h (рис.
2б). Как следует из рис. 2 б , функция  h  может быть выпуклой при   n n m
y   , и вогнутой
при   n n m
y   , .
В работе [13] предложен новый подход к определению деформации при вдавливании
сферы, в котором используется энергетическая концепция твердости [14-16]. Метод
основывается на допущении о том, что в пределах в пределах равномерной деформации при
одноосном растяжении и вдавливании шара на пластическое вытеснение части объема
материала за пределы исходного объема при одинаковой деформации затрачивается
одинаковая удельная энергия.