
Actual Problems in Machine Building. 2016. N 3
Materials Science
in Machine Building
____________________________________________________________________
484
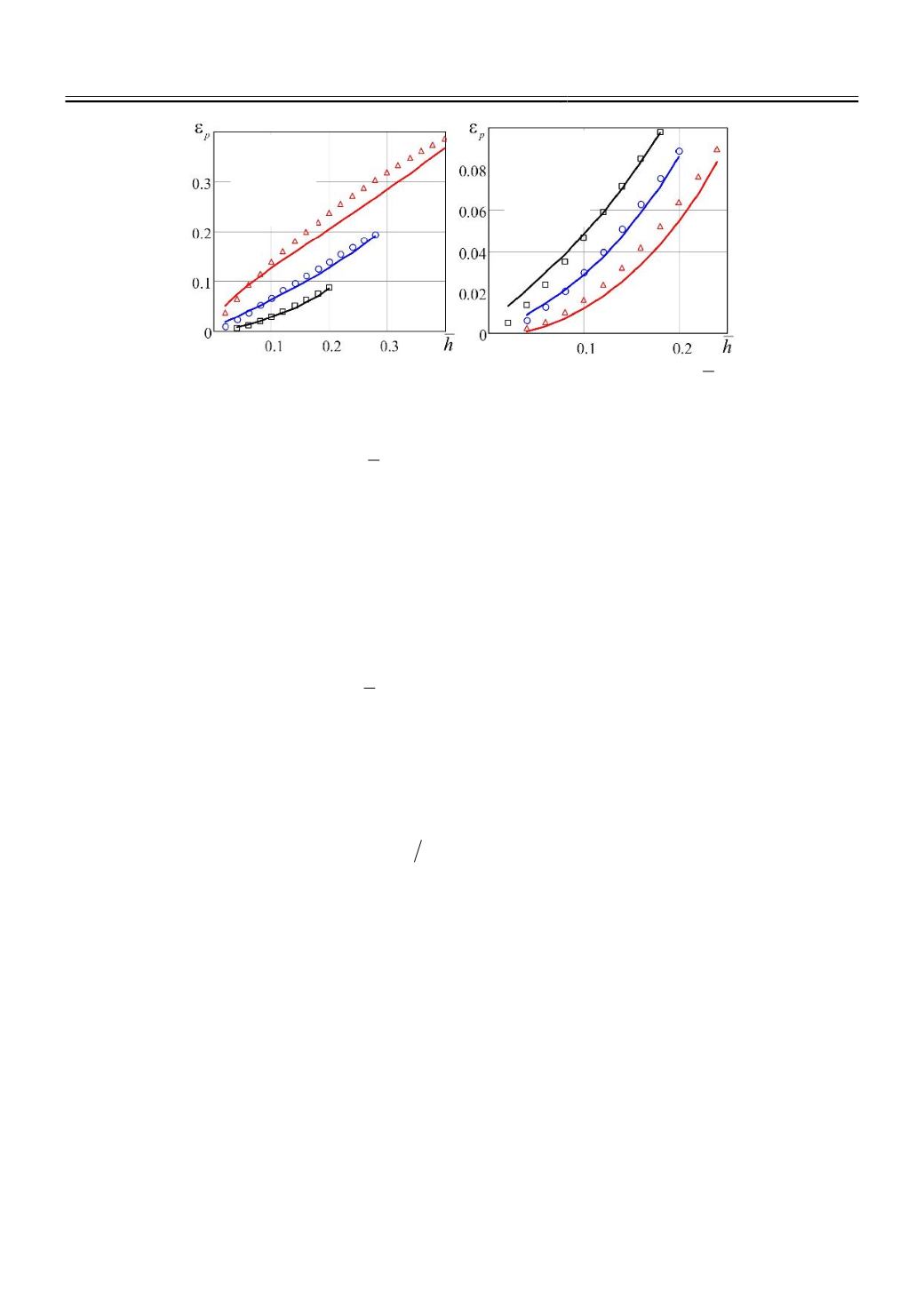
Рис. 3.
Зависимости деформации
p
от относительного внедрения сферы
h
для разных
значений
y
и
n
.
На рис. 3 сплошными линиями представлены зависимости деформации
от
относительного внедрения сферы
h
для разных значений характеристик материала
y
и
n
.
Результаты расчетов по выражению (9) приведены точками.
Заключение
1. Из приведенного обзора следует, что величина деформации при вдавливании сферы
в большинстве случаях определяется геометрическими параметрами и может отличаться в
разы.
2. Используя результаты конечно-элементного анализа для определения индекса
Майера показано, что функция
h
может быть выпуклой при
n n m
y
,
и вогнутой при
n
n m
y
2 ,
. Подход с использованием закона Майера является более информативным и
предпочтительным, так как учитывает также свойства испытываемого материала.
3. Предложен энергетический подход к определению деформации при вдавливании
сферы, при использовании которого получены близкие результаты с методом, основанном на
законе Майера. При этом индекс Майера
m
не входит в расчетные формулы в явном виде, он
используется только для определения
.
в
Ra
Список литературы
1.
Огар П.М., Горохов Д.Б
. Обзор методов определения упругопластической деформации
при внедрении сферы // Системы. Методы. Технологии. – 2015. – № 3. – С. 15–22.
2.
Ahn J.-H., Kwon D
. Derivation of plastic stress-strain relationship from ball indentations:
Examination of strain definition and pileup effect // Journal of Materials Research. – 2001. – Vol. 16. – P.
3170–3178.
3.
Марковец М.П
. Определение механических свойств металлов по твердости. – М.:
Машиностроение, 1979. – 191 с.
4.
Шабанов В.М
. Экспресс-диагностика технического состояния металла элементов
конструкций АЭС методом кинетического индентирования // Технологии техногенной
безопасности. – 2013. – № 3 (39). – С. 1–7.
ε
y
= 0,002
n
= 0,4
0,2
0,1
n
= 0,1
ε
y
= 0,001
0,002
0,003














