
Актуальные проблемы в машиностроении. 2016. №3
Технологическое оборудование,
оснастка и инструменты
____________________________________________________________________
331
колес на основе развития математических моделей напряженно-деформированного состоя-
ния металла при реализации процесса.
Материалы исследования
В основу рассматриваемой математической модели процесса профилирования было
положено численное рекуррентное решение конечно-разностной формы условия статическо-
го равновесия выделенного элементарного объема металла в очаге деформации.
Согласно принятой расчетной схемы полоса толщиной
S
подвергается поперечному
упруго-пластическому изгибу на радиус
R
. Используя принцип суперпозиционного подхода
и рассматривая с учетом этого только один участок полосы, характеризующийся наличием
постоянного по величине внутреннего радиуса кривизны
R
, осуществим разбиение всего
объема выделенного участка на конечное множество
k
Rh
элементарных объемов, имеющих
порядковые номера верхних и нижних граничных поверхностей, соответственно
j
и
(j+1)
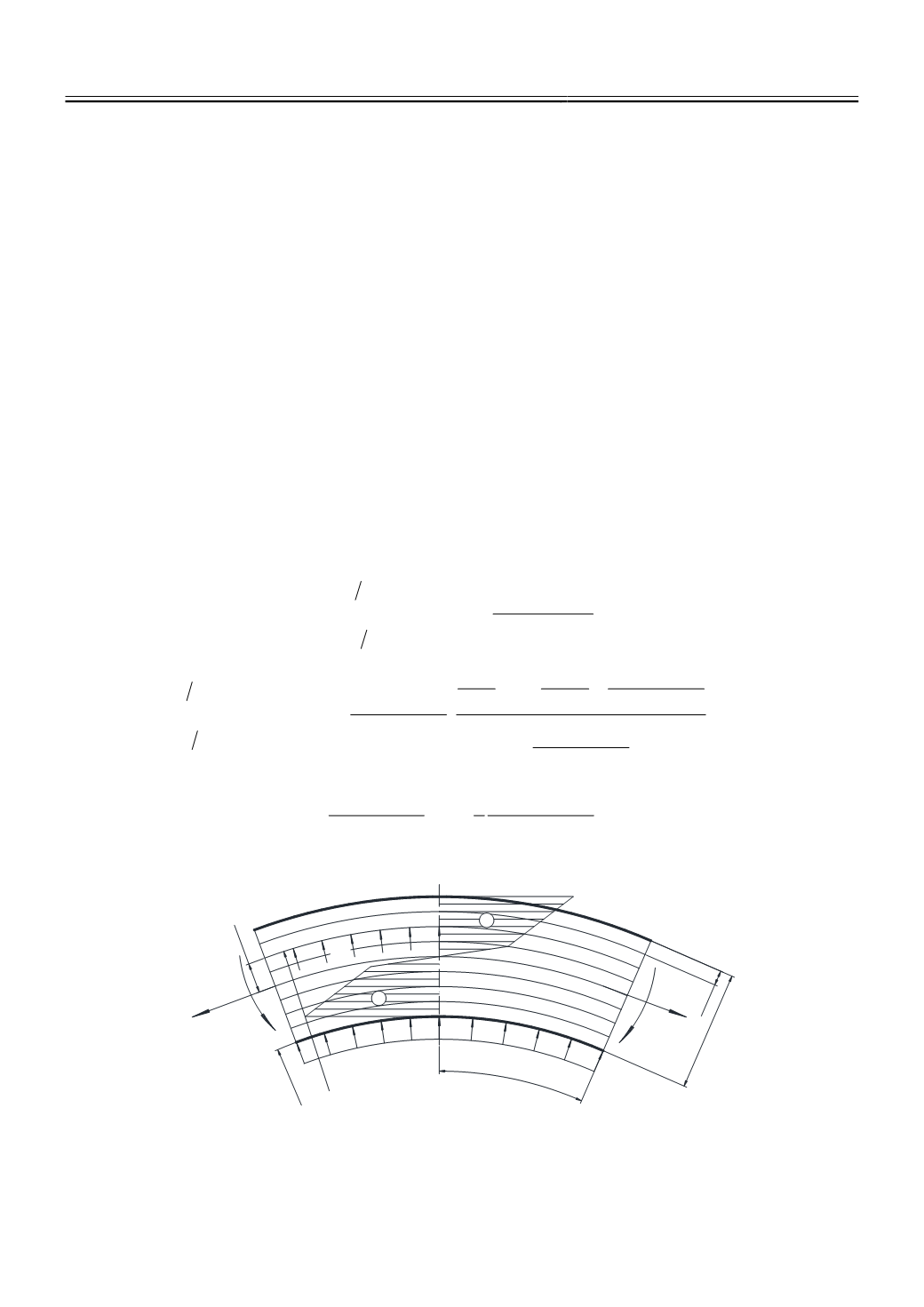
(рис. 1). Толщина каждого отдельного элементарного объема Δ
h
и геометрическая координа-
та
z
j
для каждой отдельной
j
-ой граничной поверхности с учетом условия, что начало коор-
динаты принадлежит поверхности, являющейся средней по толщине всей полосы, определя-
ется по методике, изложенной в работе [7].
Величины изгибающего момента
M
и растягивающих сил
N
можно определить по
следующим зависимостям:
2
2
1
2
1
2
S
S
k
j
j
j
z
S
dz
N
Rh
;
(1)
S z
S
S
dz z
M
j
j
j
j
j
j
S
S
k
j
j
j
z
Rh
2
2
3
2
2
2
1
1
2
2
2
2
1
2
1
S S
z
j
j
j
j
j
k
j
j
j
Rh
1
1
1
2
1
2
3
1
2
.
(2)
+
-
P
j
P
R
j
N
N
M
M
S
S
z
j
R
R
j
Рис. 1.
Расчетная схема элементарного объема при реализации процесса гибки
В самом общем случае решение уравнений (1) и (2), сводится к определению нор-
мальных тангенциальных напряжений σ
j
, неразрывно связанных с соответствующими пока-














