
Актуальные проблемы в машиностроении
. Том 4. № 1. 2017
Технологическое оборудование,
оснастка и инструменты
____________________________________________________________________
83
Уравнения движения механической системы получим на основании уравнения Ла-
гранжа второго рода [22]:
,
Ф П
i
i
i
i
i
Q
x x x
T
x
T
dt
d
N
i
, ... ,2,1
, (3)
где
Т
- кинетическая энергия системы; П– потенциальная энергия системы; Ф – диссипатив-
ная функция системы (функция Релея);
Q
i
- обобщенные силы внешних воздействий, соот-
ветствующие
i
- й обобщенной координате.
Положение устойчивого статического равновесия колебательной механической си-
стемы принимаем за начало отсчета и за нулевой уровень потенциальной энергии. В качестве
обобщенных координат, определяющих положение механической системы в пространстве,
принимаем линейные перемещения центра масс бойка
x
1
массой
m
1
, рабочего инструмента
x
2
массой
m
2
, электропривода
x
3
массой
m
3
. Под действием внешних периодических сил
f
эм1
=
f
(
i
1
,
x
1
) и
f
эм2
=
f
(
i
2
,
x
1
) в механической системе возникают сложные механические колебания.
Рассматривая реальный процесс движения, как результат совместного действия слож-
ных колебаний механической системы и периодических ударных импульсов сил, авторами
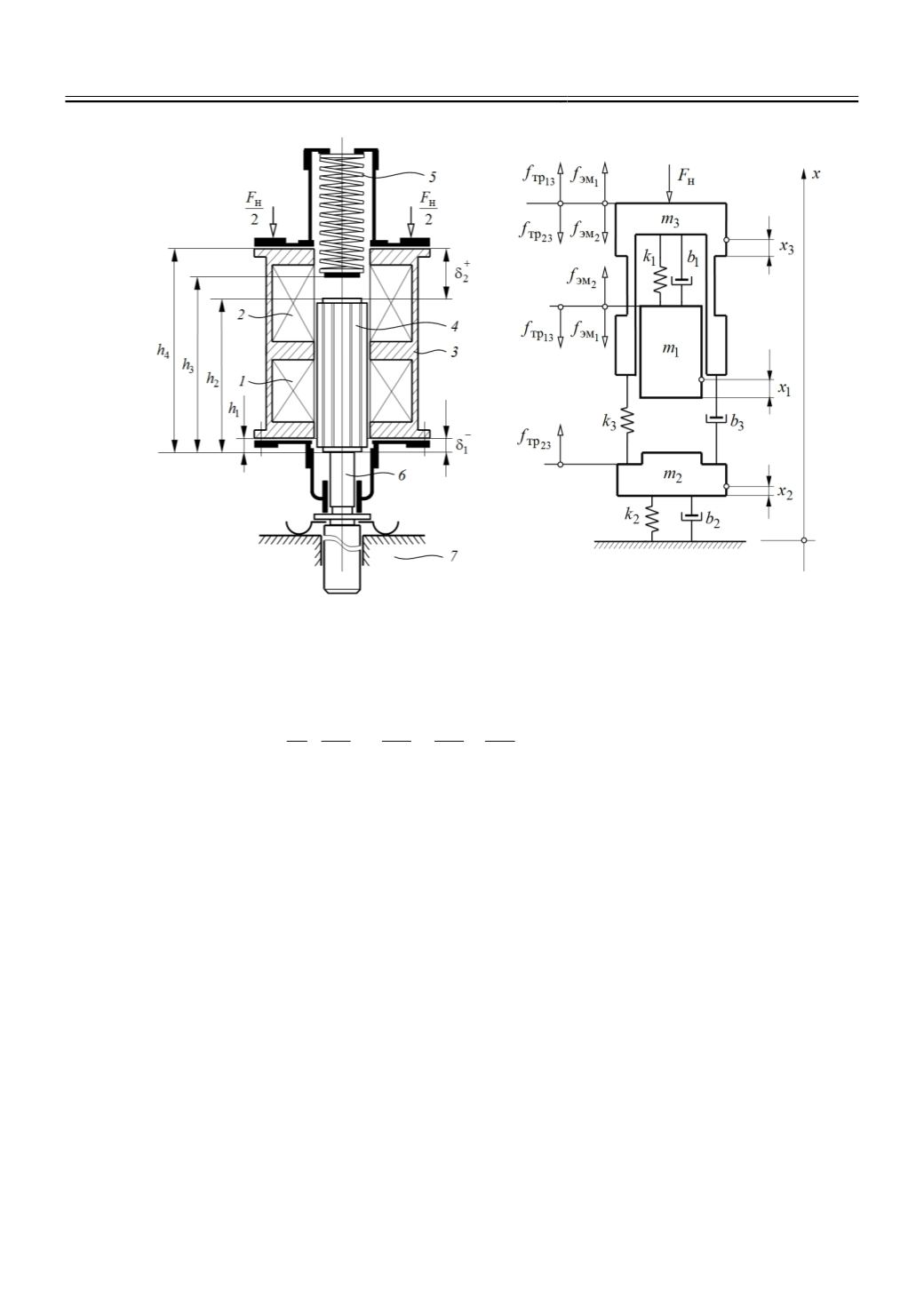
разработана обобщенная модель динамического состояния электромеханической системы
(рис. 1) [23]. Построение структурной модели динамики ударного узла и разработка алго-
ритма расчета производились в соответствии с имеющимися рекомендациями [24]. Решение
полевой части задачи выполнялось при использовании стандартной программы конечно-
элементного моделирования магнитного поля [25-27], с помощью которой определялся мас-
сив значений опорных точек статических параметров потокосцепления
1 1
1
,
x if
,
1 2
2
,
x if
и электромагнитного усилия
f
эм1
=
f
(
i
1
,
x
1
),
f
эм2
=
f
(
i
2
,
x
1
). Составляющие тока
потерь
i
п1
и
i
п2
учтены в соответствии с рекомендациями [28-29].
Рис. 1.
Электромагнитный ударный узел
Рис. 2.
Расчетная динамическая схема
механической системы
















