
Actual Problems in Machine Building. 2015. N 2
Innovative Technologies
in Mechanical Engineering
____________________________________________________________________
72
материала
и модулем упругости
Е
. На том основании, чтобы возникающие в стержне
напряжения не превзошли допускаемых, ставится условие
см
V
/ 10
max 0
.
В 1964г. Александровым Е.В. было сделано открытие [2], заключающееся в том, что
коэффициент передачи энергии ударного импульса зависит не только от массы бойка
m
и его
предударной скорости
V
0
, но и от форм соударяющихся тел. На этом основании подбор
рациональных форм бойков является одним из наиболее действенных методов
проектирования ударных систем, приводящий к увеличению значения коэффициента
передачи энергии. Имея качественные и количественные параметры импульсов, генерируемых
различными бойками, можно их сравнить с целью выявления наиболее рациональных.
Теоретические основы решения поставленной проблемы
Решение проблем, связанных с применением теории продольного удара к
исследованию машин ударного действия, естественно предполагает глубокого всестороннего
подхода к выбору методик, которые бы в наибольшей мере соответствовали физическим
особенностям рассматриваемой ударной системы. Среди известных, апробированных
методов исследования продольного соударения стержней [3] наиболее широкое применение
получила одномерная волновая теория Барре де Сен-Венана [4], построенная для стержней с
плоскими торцами на тех допущениях, что: 1) плоские, поперечные к оси стержня сечения
остаются плоскими в процессе распространения волн продольной деформации; 2) материал
стержня подчиняется закону Гука, т.е. деформации остаются в пределах упругости; 3)
соприкосновение соударяющихся тел происходит в один и тот же момент времени по всей
площади ударного торца. По теории Сен-Венана процесс распространения волн продольных
колебаний в стержне постоянного поперечного сечения описывается дифференциальным
уравнением
2
,
2
2
2
,
2
x
u
a
t
u
tx
tx
,
(1)
где
u
(
x,t
)
– функция смещения поперечного сечения стержня с координатой
х
в момент
времени
t
.
О возможности решения задач продольного соударения стержней с помощью
уравнения (1) показывается также в известных работах Лява А., Кольского Г., Геронимуса
Я.Л., Кильчевского Н.А., Кошлякова Н.С., Алимова О.Д., которые показывают, что при
продольных колебаниях стержней постоянного поперечного сечения можно пренебречь
поперечными колебаниями без существенных ошибок, а продольный импульс
распространяется вдоль стержня без изменения формы.
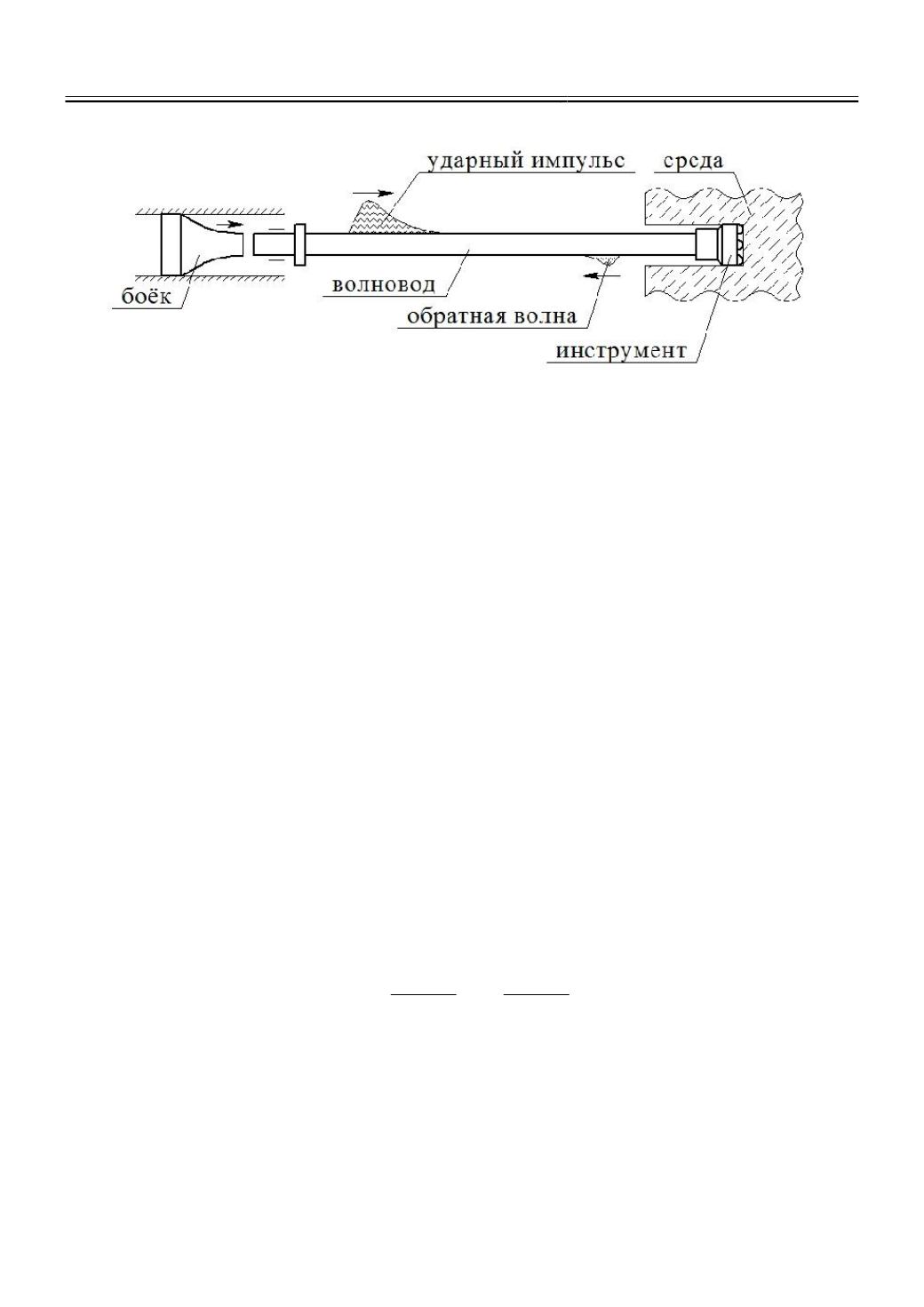
Рис. 1.
Схема ударной системы технологического назначения

















