
Actual Problems in Machine Building. 2015. N 2
Technological Equipment, Machining
Attachments and Instruments
____________________________________________________________________
214
нитного двигателя, обеспечивающих минимальную массу, при заданном значении амплиту-
ды тягового усилия. При выводе основных расчетных формул использовались известные ре-
шения, приведенные в работах [23, 24].
Математическая постановка задачи заключалась в нахождении значений переменных
Y
1
,
Y
2
…
Y
n
,
которые
минимизируют
массу
электромагнитного
двигателя
1 2
( , ,.., )
n
M f Y Y Y
в заданном диапазоне значений амплитуды тягового усилия
min
1 2
max
( , ,.., )
э
э
n
э
F F Y Y Y F
.
Алгоритм расчета следующий:
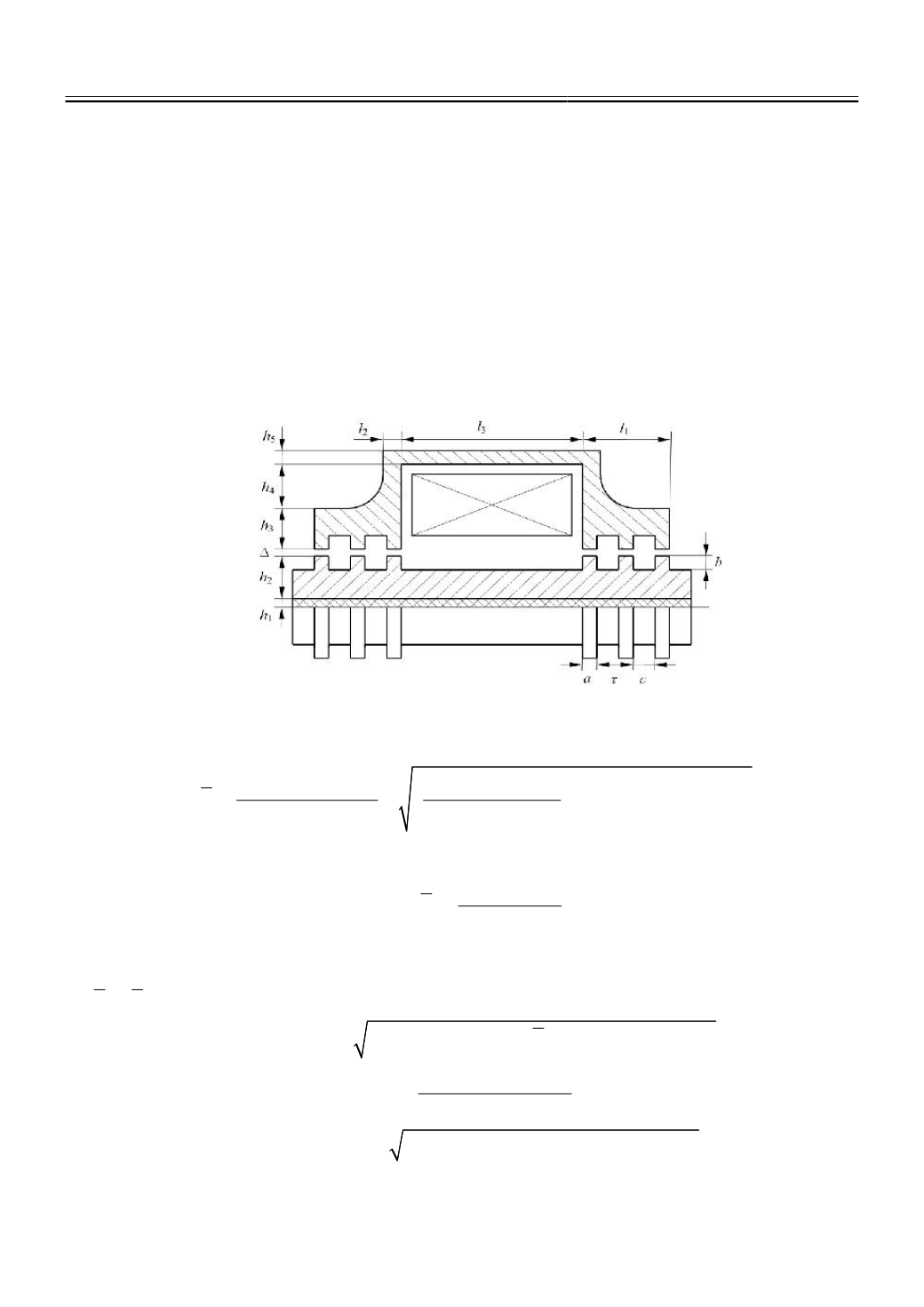
1. На первоначальном этапе задаются основные геометрические размеры двигателя:
ширина немагнитной втулки
h
1
, длина окна катушки
l
3
, ширина зубца
a
и межзубцового про-
странства
c
, высота зубца
b
, ширина воздушного зазора
и число пар зубцов одного полюса
n
(рис. 1).
Рис.1.
Конструктивная схема электромагнитного двигателя в разрезе
2. Исходя из равенства сечений отдельных элементов магнитопровода [8], определя-
ется усредненное значение высоты якоря:
2
2
1
1
2
1
1
1
(2 2 )
(2 2 ) (
2 2 )
2
4
h b an
h b an
h Y
b h b anh
(1)
3. Далее, исходя из конструктивных соображений, определяется усредненное значе-
ние высоты ярма статора
h
4
:
2max
2min
4
2
2
Y Y
h Y
(2)
4. Из условия равенства сечений якоря
S
я
, ярма
S
яс
и полюсного наконечника статора
S
пн
находятся значения
5
3
h Y
,
2
4
l Y
и
3
5
h Y
, выраженные через усредненные значения
1
Y
и
2
Y
:
2
2
2
3
1 1
5
2
1 1
5
2
1 1
1
(
)
(
) (
)
Y h Y Y Y
h Y Y Y h Y h
(3)
2
2
1 1
1
4
1 1
5
(
)
2(
)
h Y h
Y
h Y Y
(4)
2
2
5
1
2
1
2
2
1 2
(
) (
) (
2 2 )
Y h h
h h
h h h b
(5)

















