
Материаловедение, динамика и прочность машин и механизмов
217
p
n
T
в
p
T p
в
e
n
1ln 500 ln
ln
0002 ,0
1ln ln
1 ln
;
(20)
0
ln ln
215 ,5
T
в
n nn
.
(21)
Ранее аналогичное выражение было получено в работах [22, 23].
Таким образом, используя характеристики σu и σ02 (или σu и σy) условной диаграммы растя-
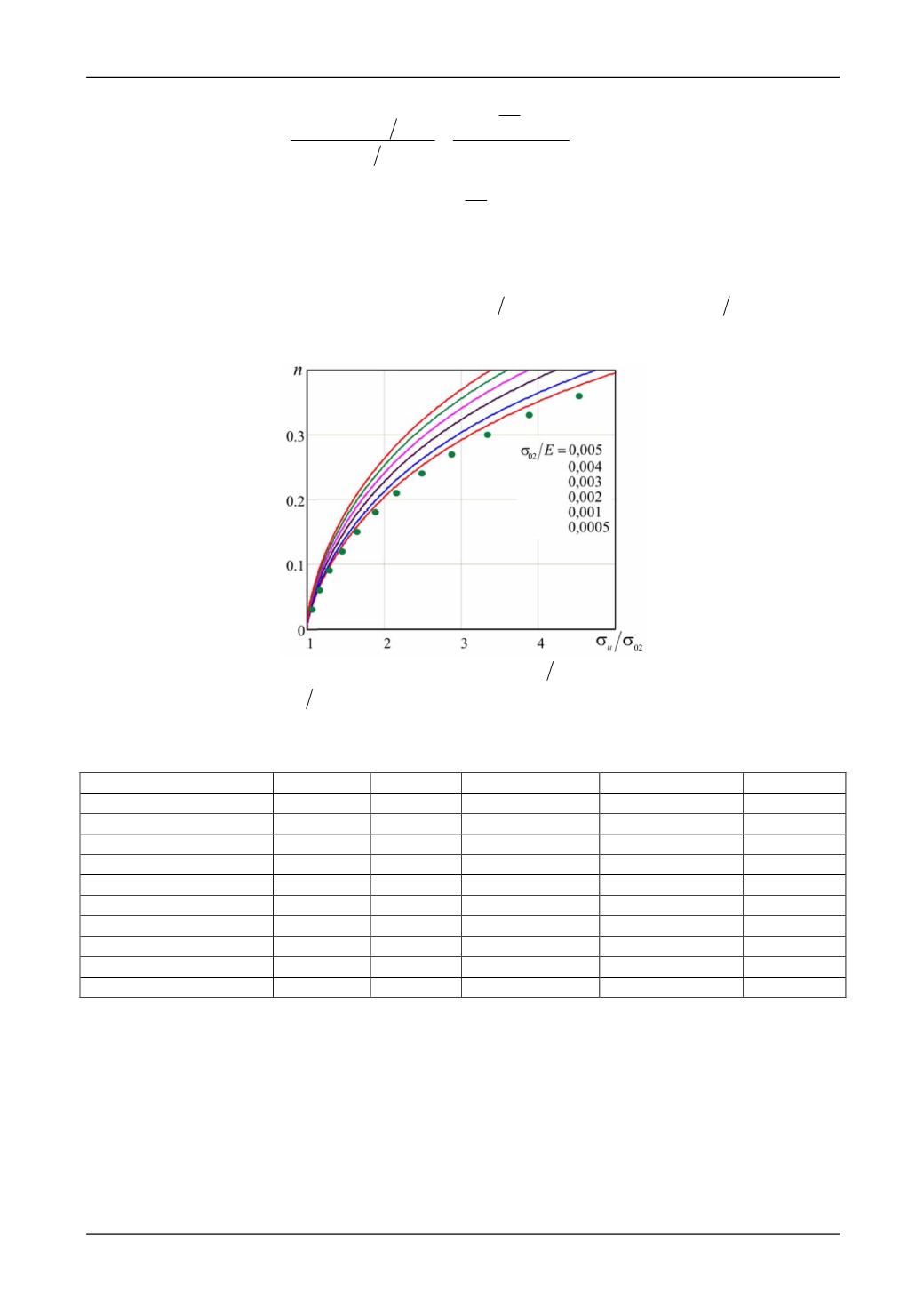
жения, из уравнения (15) (или (18)) определяем экспоненту упрочнения n. На рис. 2 представлена за-
висимость экспоненты упрочнения
n
от отношения
02
u
для разных значений
E
02
, определен-
ная из выражения (15).
Рис. 2. Зависимость экспоненты
n
от отношения характеристик
02
u
условной диаграммы растяжения при
значениях
005 ,0...
0005 ,0
02
E
. Точками обозначена зависимость (21).
Таблица. 2.
Параметры упрочнения
Материал
n
n
f
S
u
, МПа
S
uf
, МПа
γ, %
Ст3
0.212
0.197
613
576
6.05
09Г2С
0.177
0.164
613
584
4.69
45
0.16
0.16
664
663
0.17
22К
0.206
0.164
679
570
16.09
16ГНМ
0.176
0.156
678
627
7.62
10Х2М
0.083
0.147
700
841
-20.1
12Х2МФА
0.124
0.159
784
881
-12.35
12Х18Н9
0.257
0.233
812
730
10.07
25Х2М1Ф
0.103
0.136
1107
1213
-9.54
27Х2Н2МФВ
0.077
0.071
1397
1377
1.42
Случай 3. Заданы:
02
,
u
,
E
,
f
.
В этом случае экспонента упрочнения
n
f
определяется выражениями (11) и (10).
В таблице 2 для материалов, указанных в таблице 1, приведены расчетные значения экспо-
нент упрочнения
n
и
n
f
, а также зачения истинных напряжений
S
u
и
S
uf
для
n
u
и относительное
расхождение γ между ними.
Заключение.
1.
При определении экспоненты упрочнения следует учитывать на пределе текучести оста-
точную деформацию 0,2 %.
2.
Приведенное выражение для определения экспоненты упрочнения, содержащее отноше-














