
Actual Problems in Machine Building. 2015. N 2
Technological Equipment, Machining
Attachments and Instruments
____________________________________________________________________
326
Для транспортировки груза по канату, натянутому в пролете между двумя опор-
ными точками, необходимо обеспечить траекторию его движения определенной формы.
Вес груза будет влиять на траекторию его движения и силу натяжения каната, изменяя
условия транспортировки и силовую картину процесса [1, 2]. При разработке канатного
спуска необходимо решить ряд вопросов, в том числе, по определению рациональной
траектории движения груза ограниченной массы с возможностью автоматического тор-
можения в конечной точке траектории.
Целью исследований являлась количественная оценка влияния веса груза и его по-
ложения на траекторию движения и силу натяжения каната, а также доказательство возмож-
ности упрощения поиска рациональной траектории движения груза по канатному спуску.
Теория
Расчетная модель движения груза по канатному спуску представляет собой механи-
ческую систему в виде материальной точки массой
m
, движущейся в вертикальной плос-
кости по упругой нити, натянутой между опорными точками
А
и
В
, отстоящими друг от
друга на расстоянии
l
(рис. 1).
Будем считать, что вследствие упругой деформации нити точка
С
подвеса груза
расположена по горизонтали на расстоянии
х
от опоры
А
. Стрела провеса нити в точке
С
равна
f
.
Первоначальное натяжение нити без учета собственного веса имеет значение
Т
0
. В
результате действия веса груза оно изменится на величину
T
и будет равно
Т.
Таким об-
разом,
T = Т – Т
0
.
Обозначим отношение
l
x
.
Длины ветвей деформированной нити могут быть представлены:
,
1
J
T l
J
xT x AC
( 1 )
,
1 1
J
T
l
J
x l T x l
BC
( 2 )
где:
J
=
E
A
– жесткость сечения нити;
Е
и
А –
модуль упругости материала нити и площадь
ее поперечного сечения.
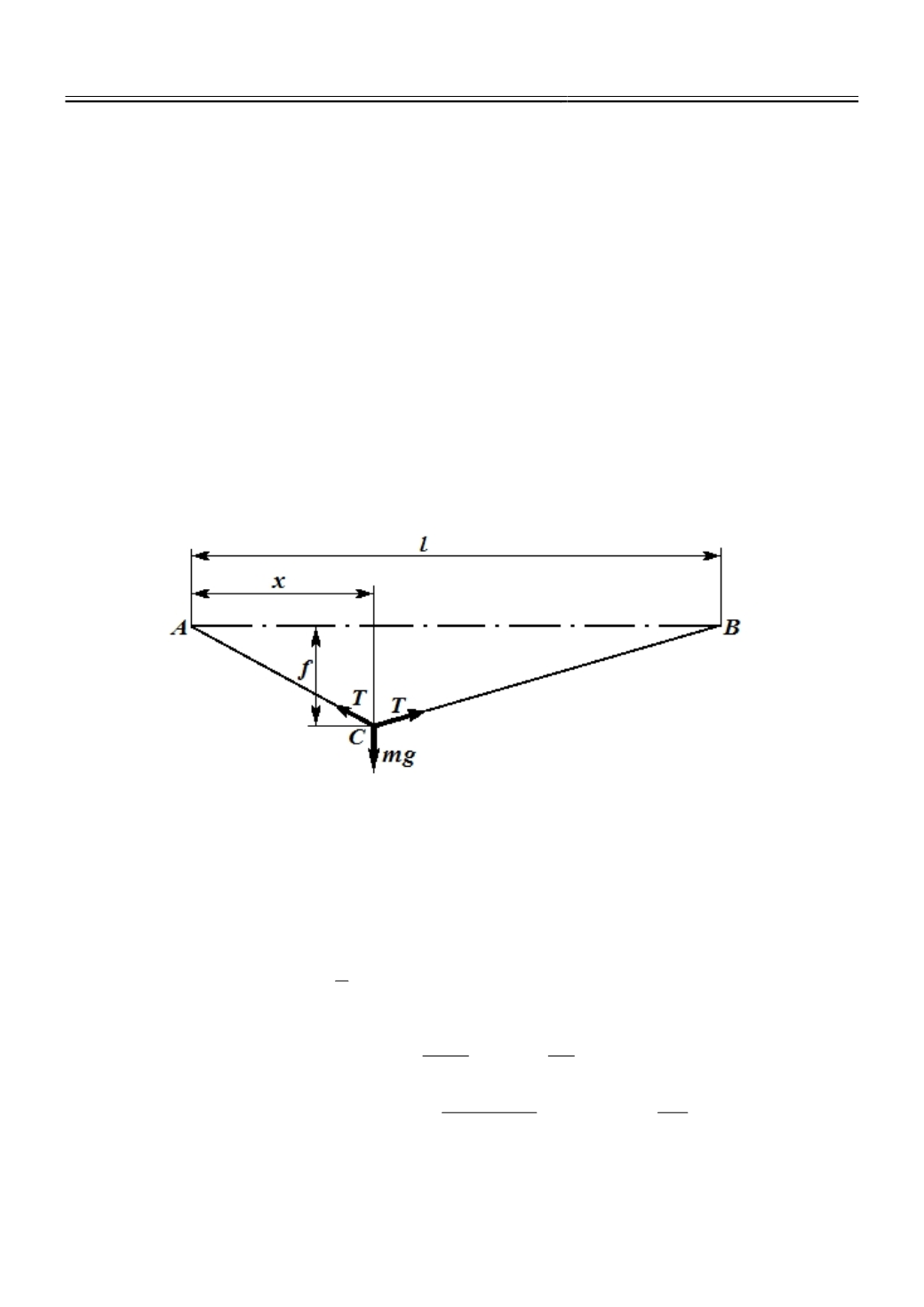
Рис. 1.
Схема подвеса груза массой
m
на упругой нити.

















